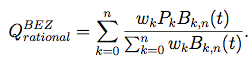
Racionální Bézierovy křivky patří do skupiny parametrických křivek, které se vytvářejí pomocí řídících bodů. Bézierovy křivky mají velkou nevýhodu a to tu, že pomocí nich nejsme schopni sestrojit ani jednoduché tvary a kuželosečky, jako jsou kružnice, elipsa apod. Snaha vyřešit tento nedostatek vede k použití konceptu váhy u každého řídícího bodu.
Pokud chceme zvolit řídící body pro racionální Bézierovu kubiku, provedeme to kliknutím do vykreslovací plochy vpravo nahoře. Kubika je určena čtyřmi body, tedy klikneme čtyřikrát. Poté se nám vykreslí zadaná křivka a ihned můžeme vidět její parametrický rozklad. Ovládací zaškrtávací tlačítka nám umožní zapínat a vypínat polynomy a bod na křivce. Nastavováním posuvníku čas t určujeme pozici zobrazeného bodu na křivce od začátku do konce křivky. Pro tuto operaci však musíme mít zaškrtlé políčko zapnout bod na křivce. Váhu bodů změníme tak, že klikneme na jeden z nich levým tlačítkem myši, bod se aktivuje a vybarví červeně. Posuvník vlevo dole se nám aktualizuje na váhu daného bodu a my ji můžeme měnit. Okamžitě tak vidíme, jak se celá křivka mění a s ní samozřejmě racionální Bersteinovy polynomy, ze kterých jsou průběhy jednotlivých souřadnic složeny.
Racionální Bézierovy křivky jsou zobecněním Bézierových křivek. Bézierovy křivky jsou zvláštním případem racionálních, když jsou všechny váhy w rovny jedné. Racionální Bézierova křivka je dána vztahem:
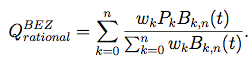
Zde wk jsou váhy, řídící body Pk a Bernsteinovy polynomy n-tého řádu Bk,n. Řídicí bod k sobě „přitahuje“ křivku určitou „silou“, která je úměrná váze w. Na problematiku by se dalo dívat i tak, že bod s vyšší váhou má vyšší důležitost a křivku v daném místě ovlivňuje více než body s nižší váhou. Výhodou je pak možnost manipulace s tvarem křivky bez změny polohy řídících bodů.
Pro rasterizaci Bézierových křivek/ určení jejích bodů lze využít de Boorův algoritmus, který obdobně jako algoritmus de Casteljau pracuje rekurzivně.
(c) 2012–13 Jakub Malina, Pavel Rajmic, Ústav telekomunikací, FEKT, VUT v Brně