Supplementary web page to the paper

Orthogonality is Superiority in Piecewise-polynomial Signal Segmentation and Denoising

The above-titled paper has been submitted (June 2018) to EURASIP Journal on Advances in Signal Processing.
This webpage serves as supplementary to this paper, in sense of the reproducible research idea.

Abstract

Segmentation of signals often relies on the polynomial model which assumes that every segment is a polynomial of certain degree, and that the segments are modeled independently of each other. Segment borders (breakpoints) correspond to positions in the signal where the model changes its polynomial representation. In this letter we show that using orthogonal polynomials instead of other systems in the model is beneficial when signals corrupted by noise are due to segmentation. The switch to orthogonal bases brings better resolving the breakpoints, it removes the need for including additional parameters and their tuning, and it brings numerical stability. And, it comes for free!

Data and codes

The archive with data and Matlab codes ready to be run. Read the readme file.

Plots

Due to space limitations, there are only selected examples of the results in the paper. The complete list of plots follows.

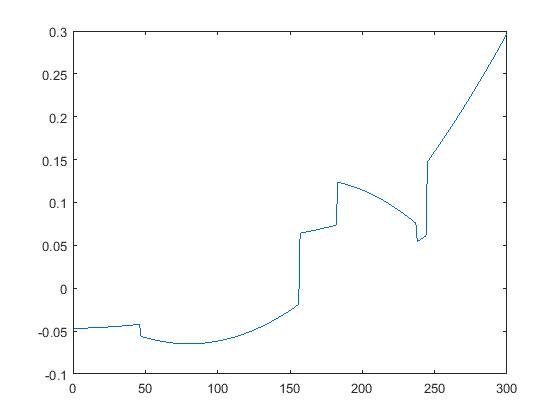
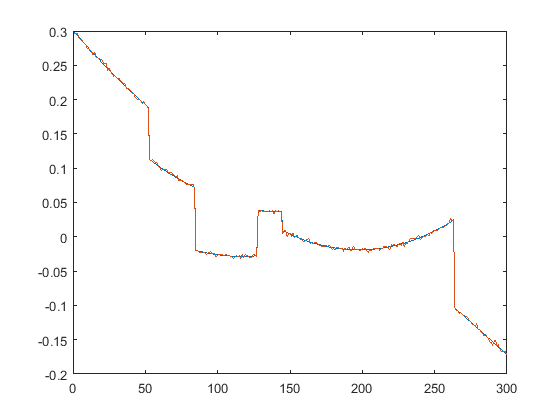
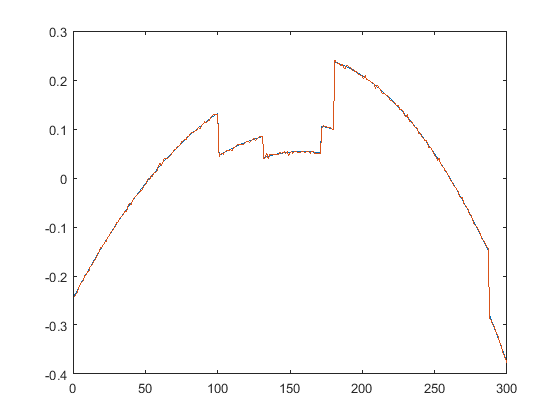
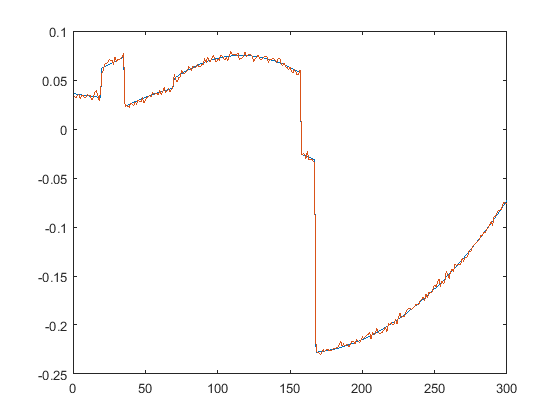
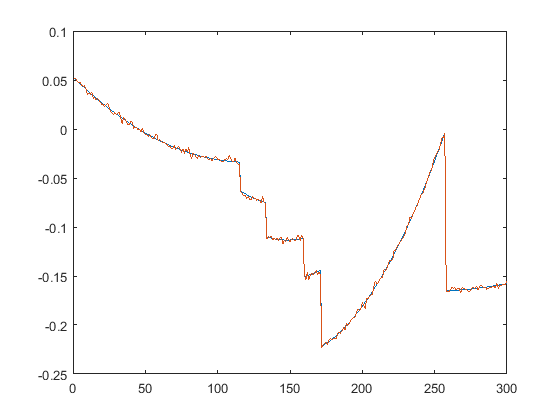
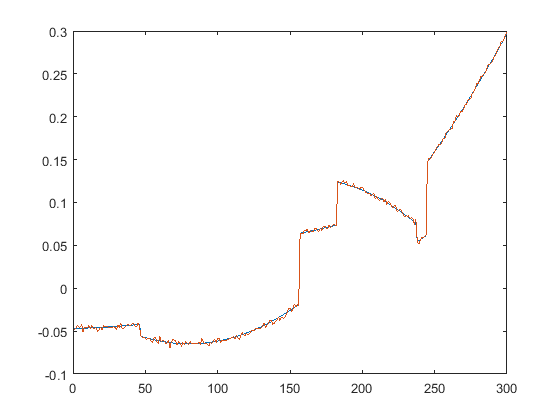
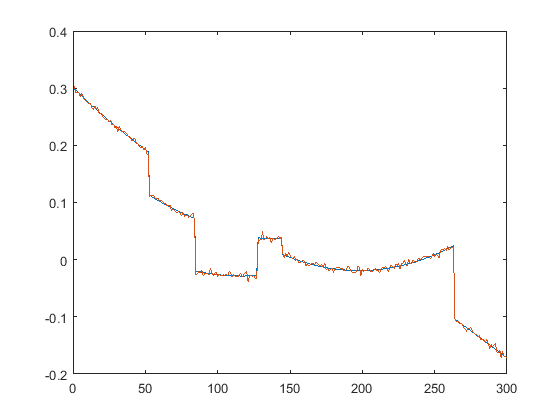
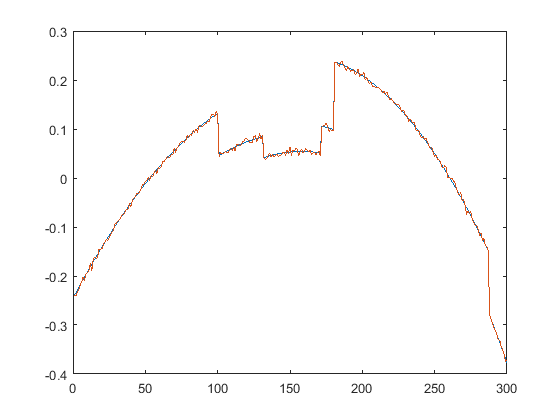
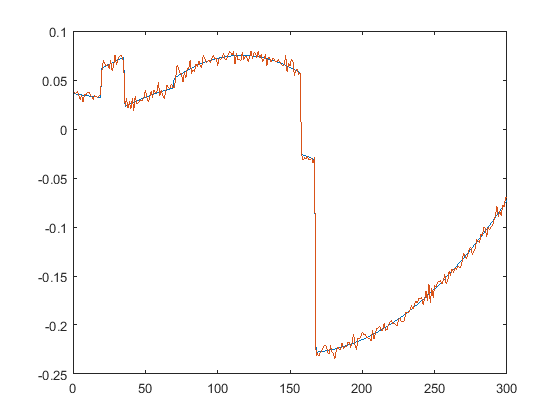
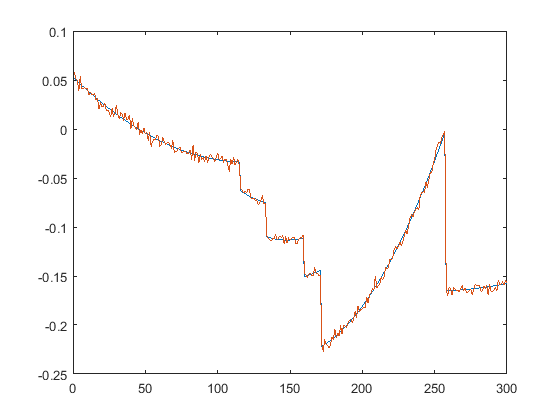
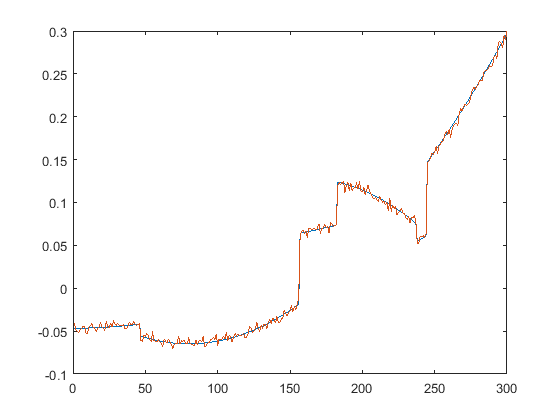
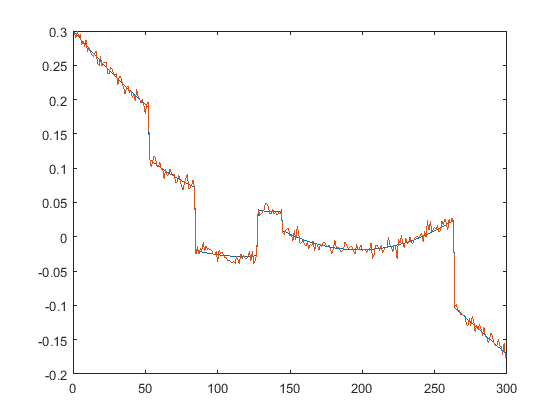
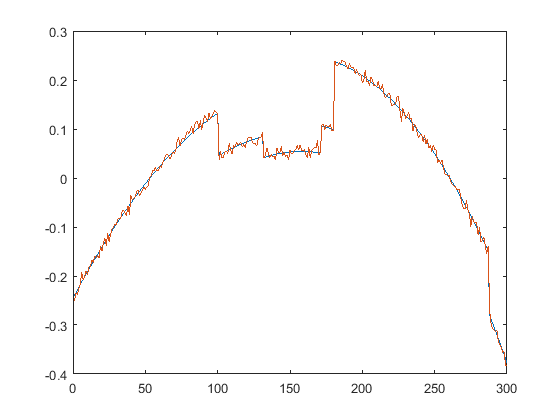
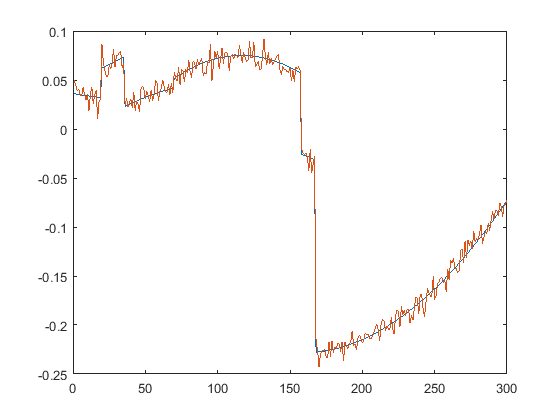
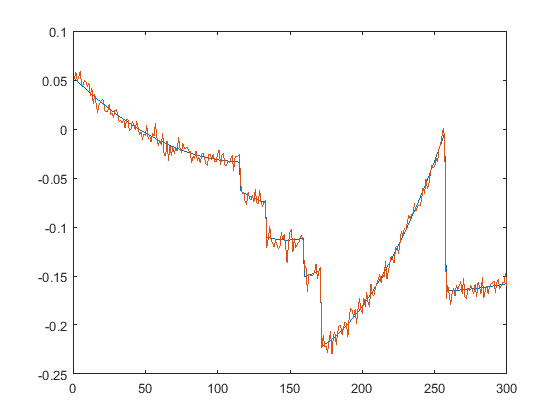
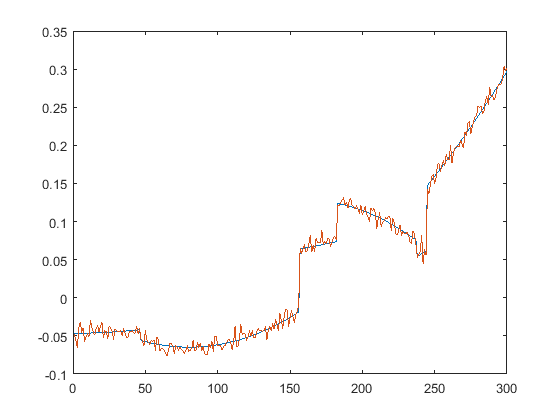
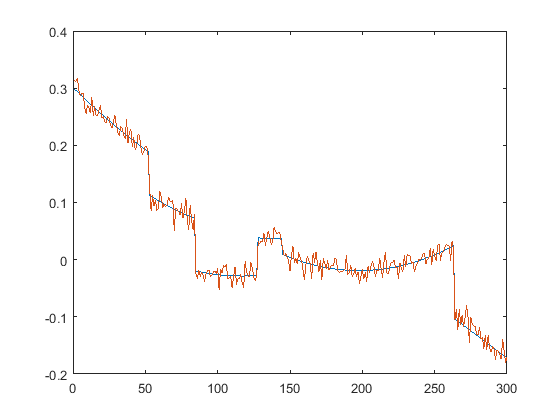
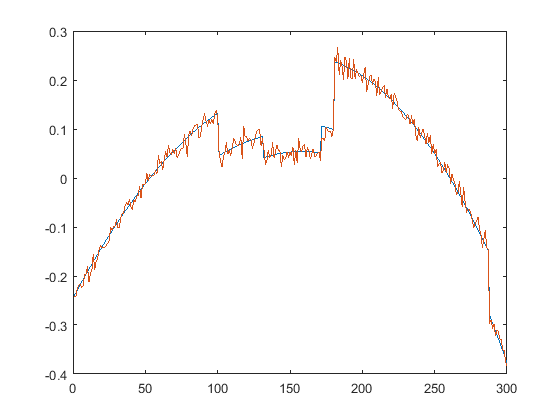
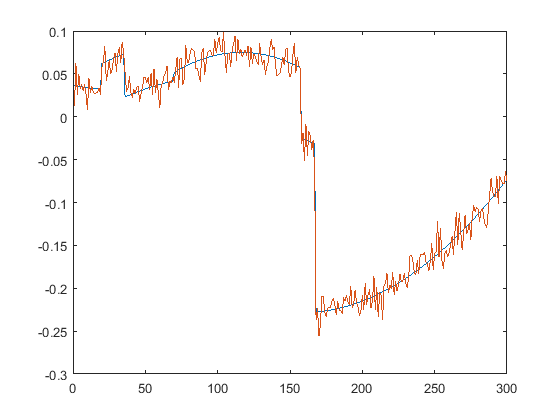
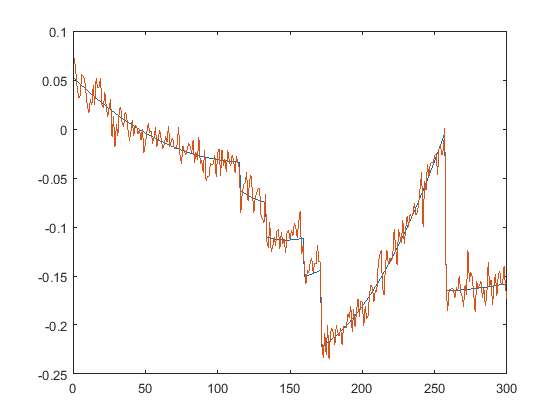
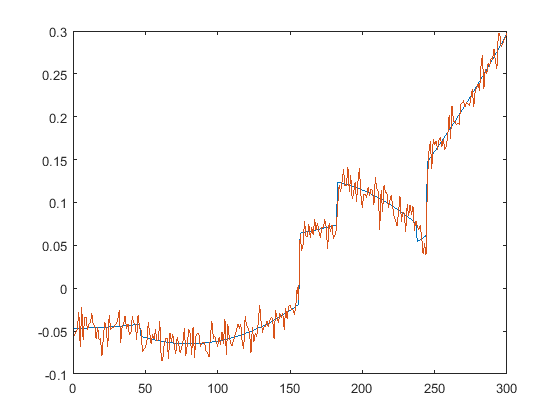
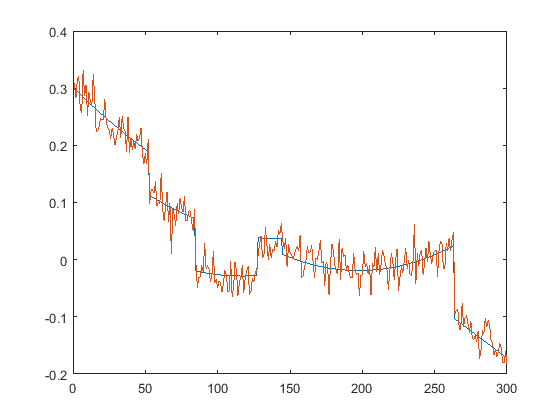
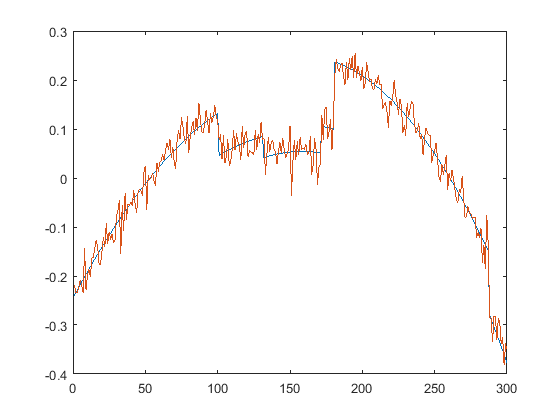
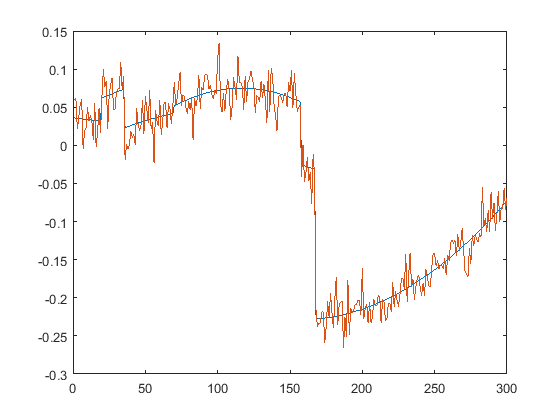
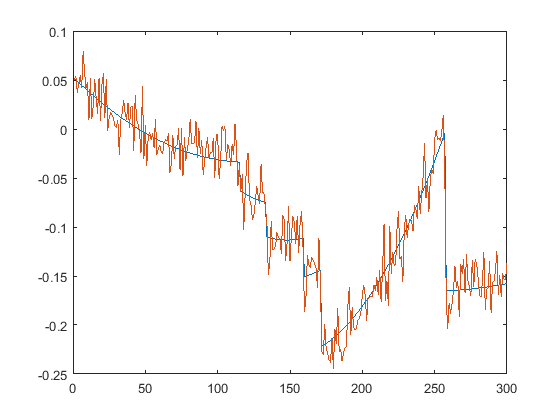
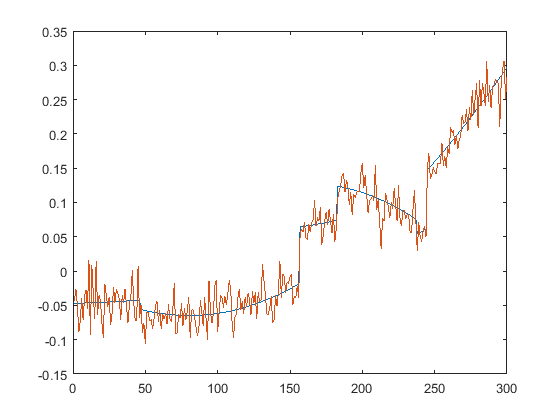
First we present the five test signals:

Next, we plot the signals with (one realization of) noise of different SNRs (from top to bottom, 35, 30, 25, 20, 15 dB):

Next, the distribution of the delta parameter used in the optimization problem is depicted, for SNRs 35, 30, 25, 20, 15 dB:

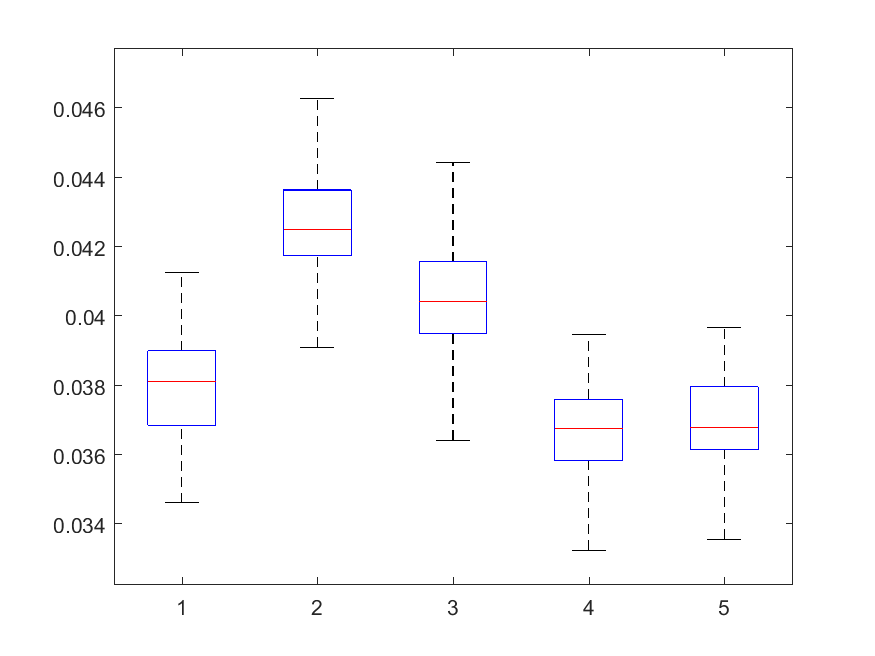
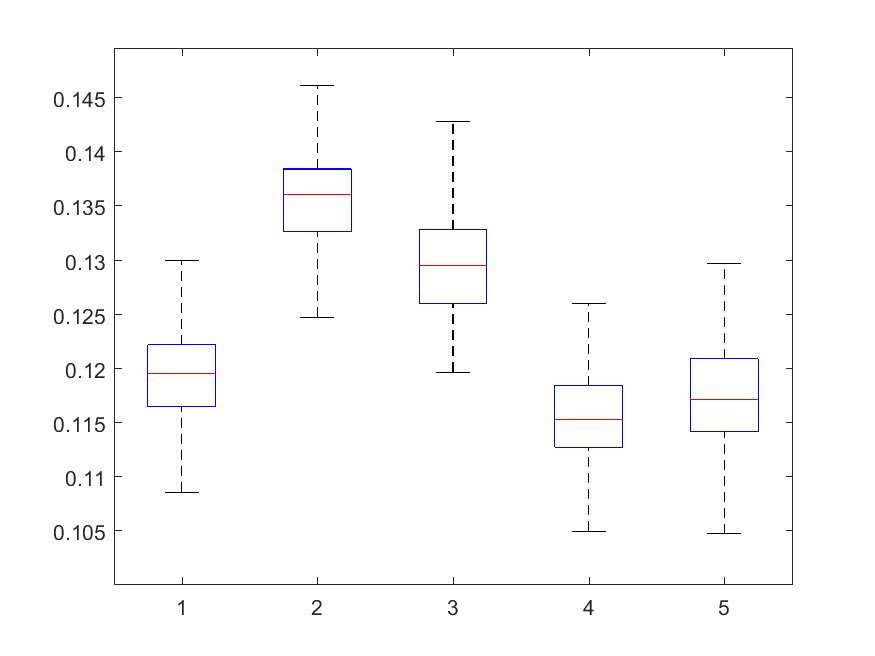
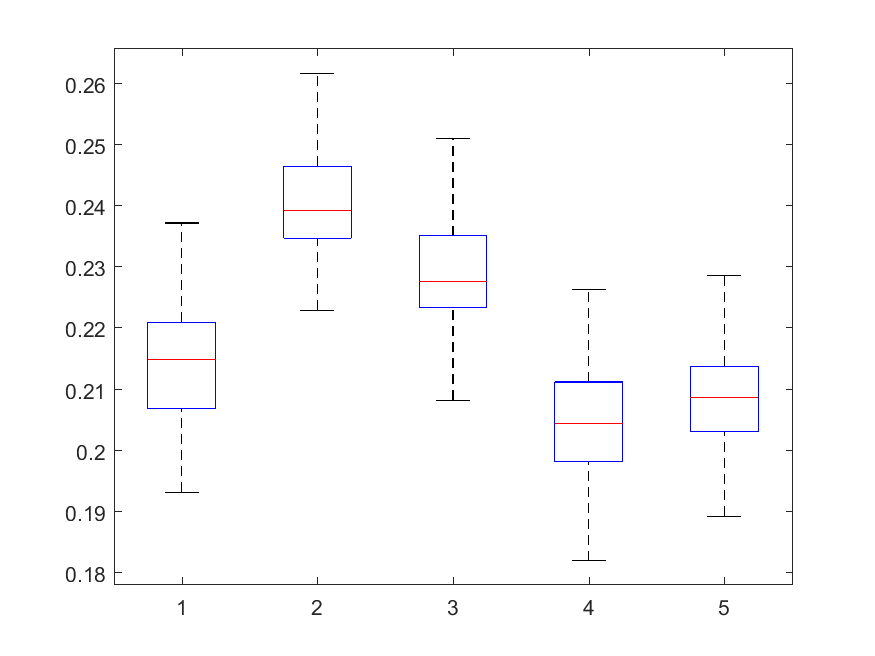
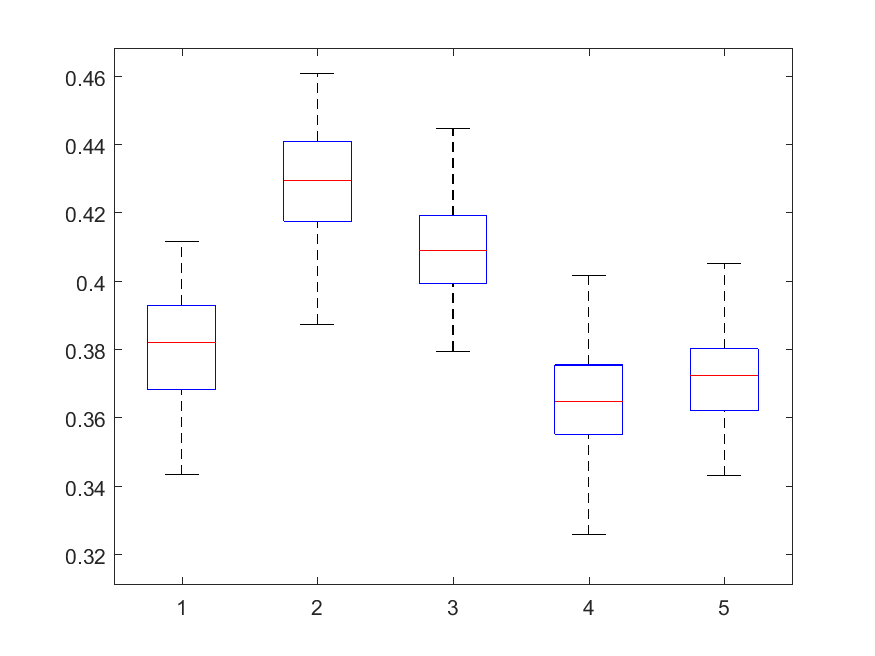
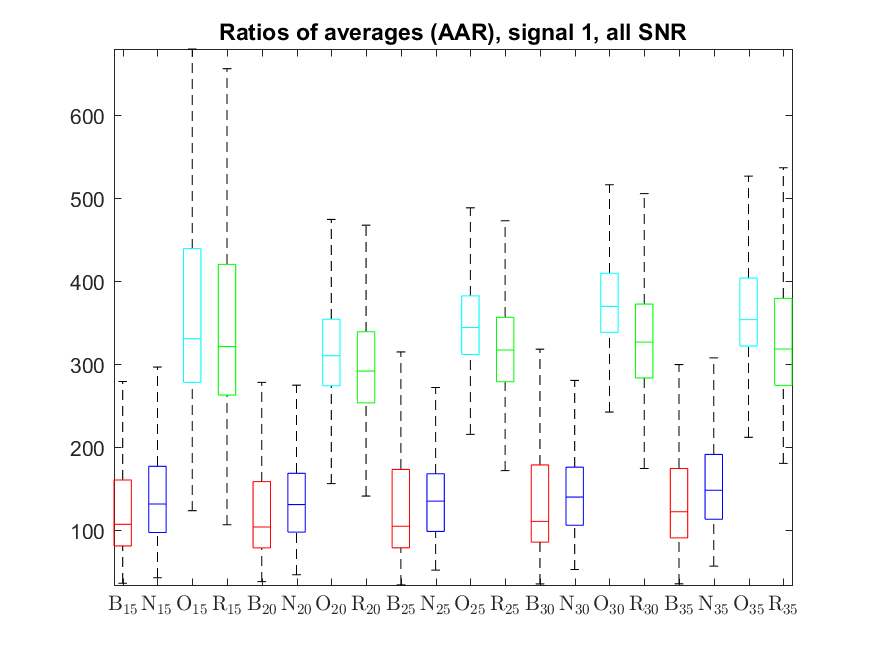
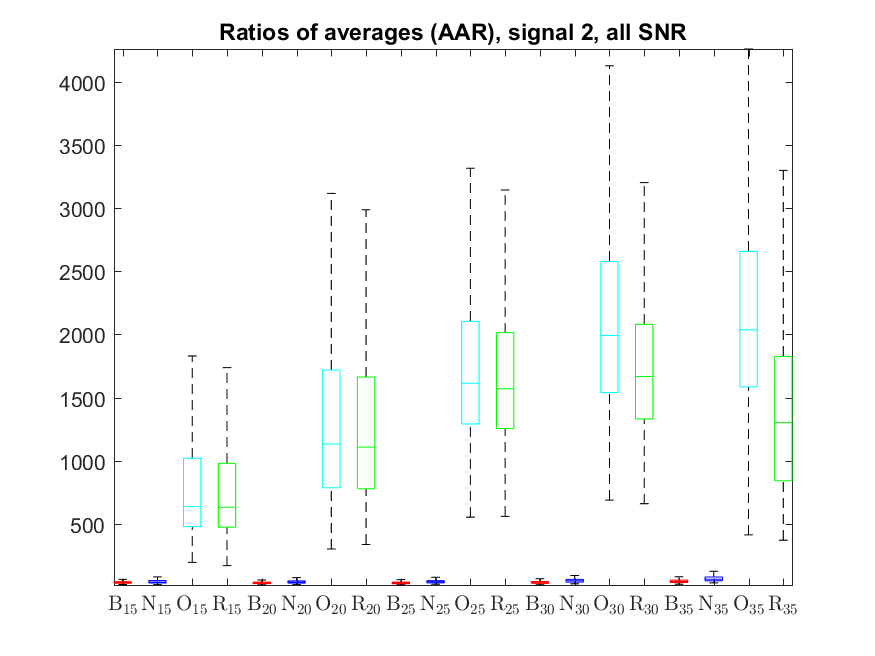
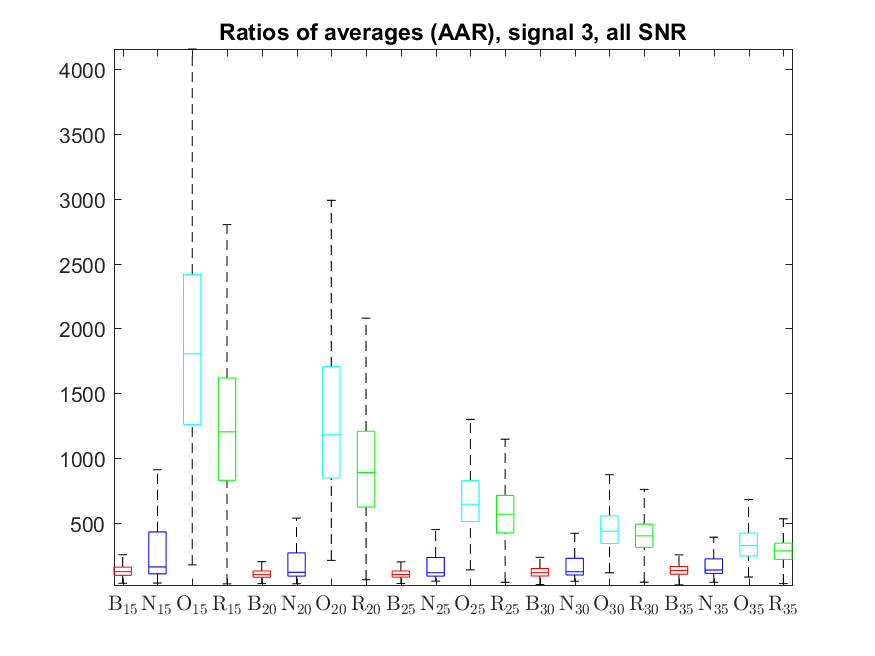
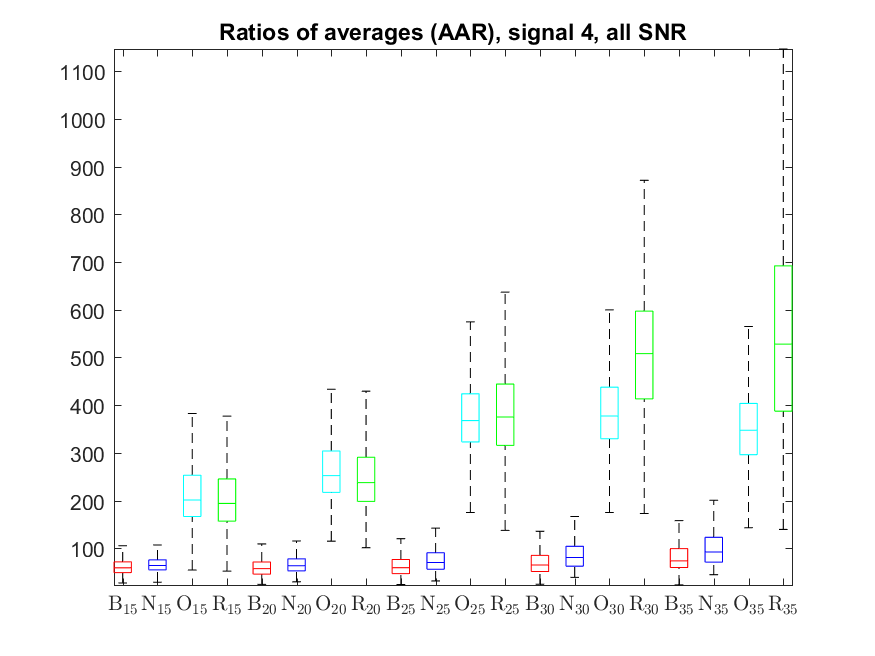
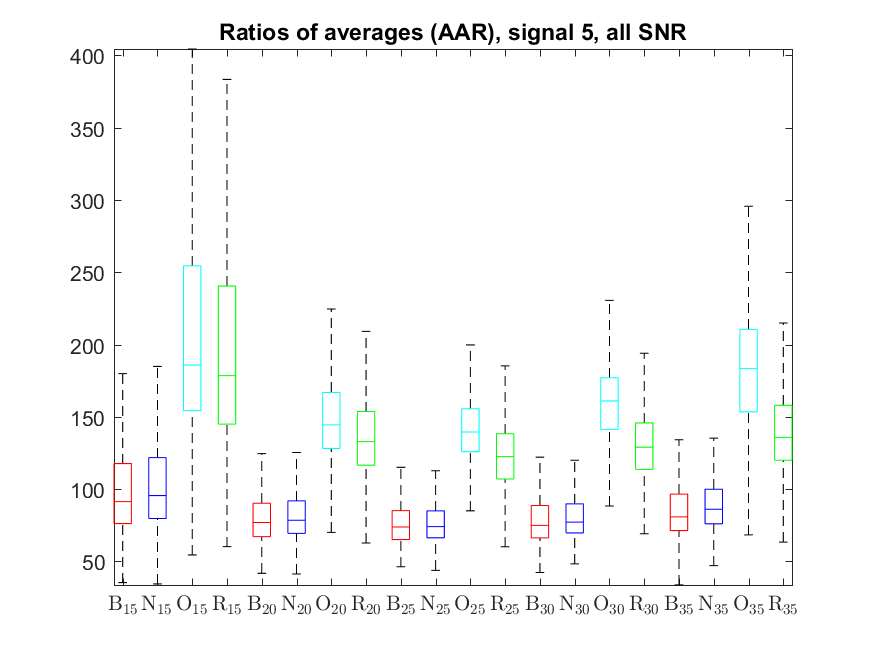
The following box-plots present the distribution the AAR indicator, as defined in the paper:

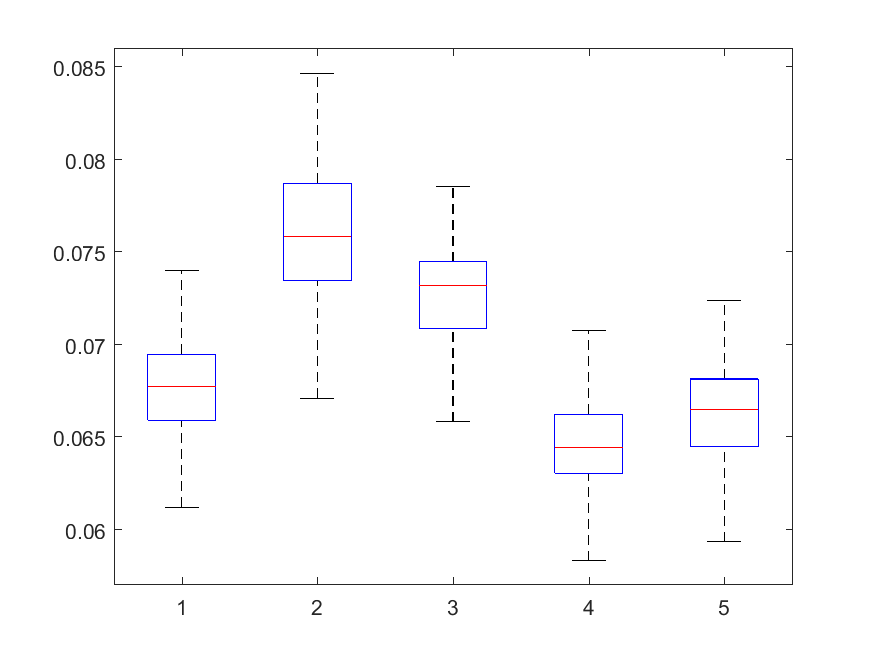
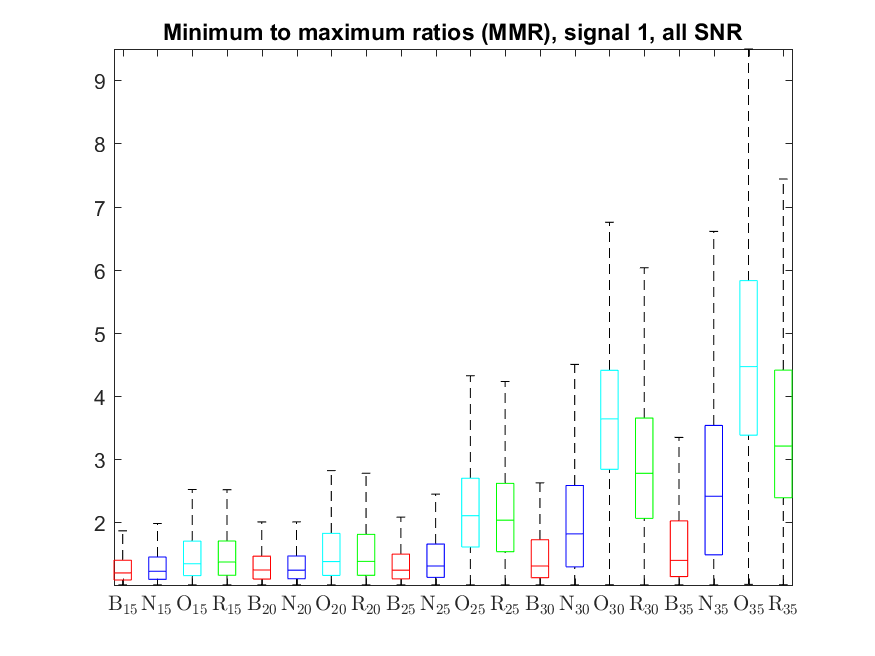
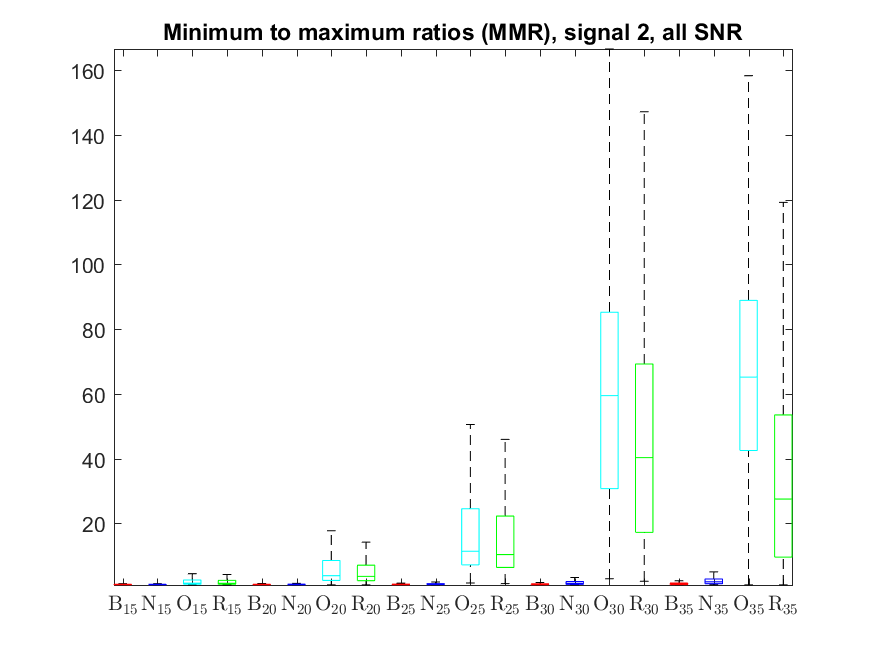
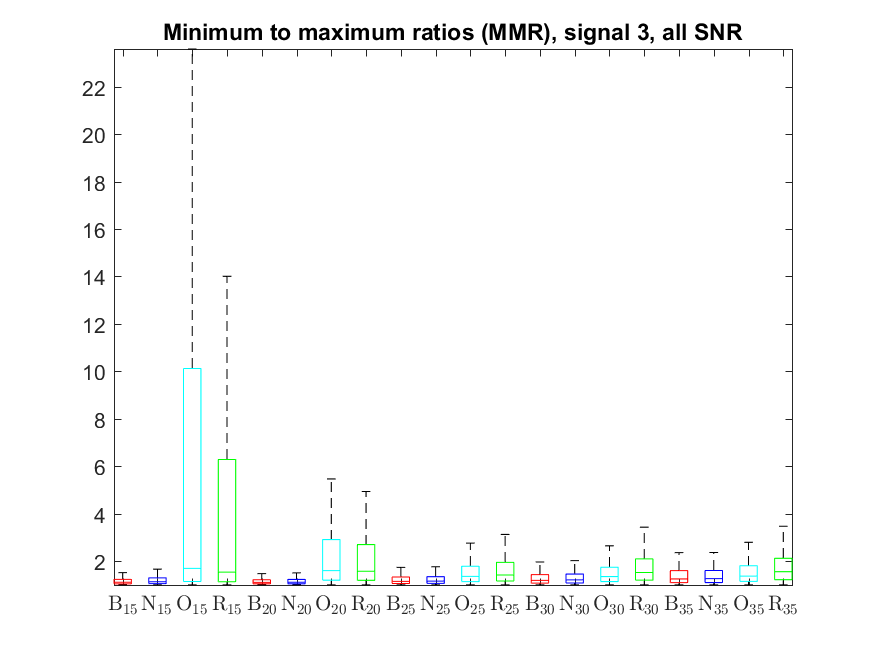
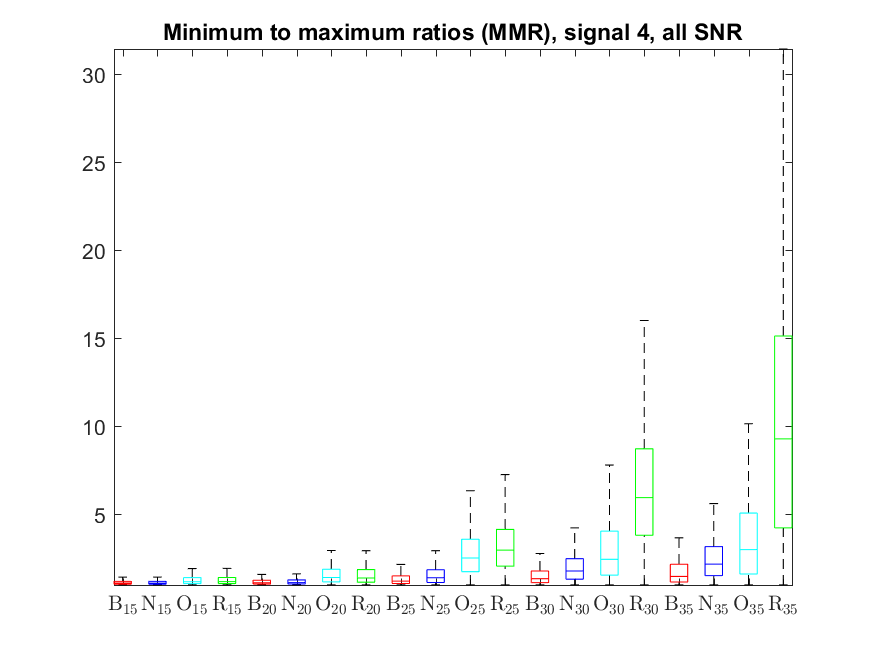
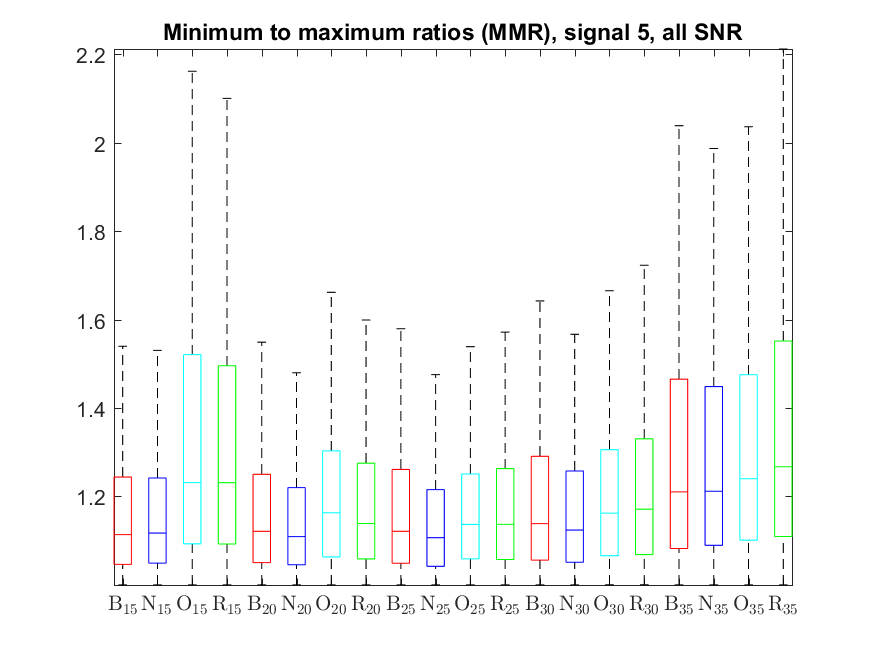
The MMR indicator follows:

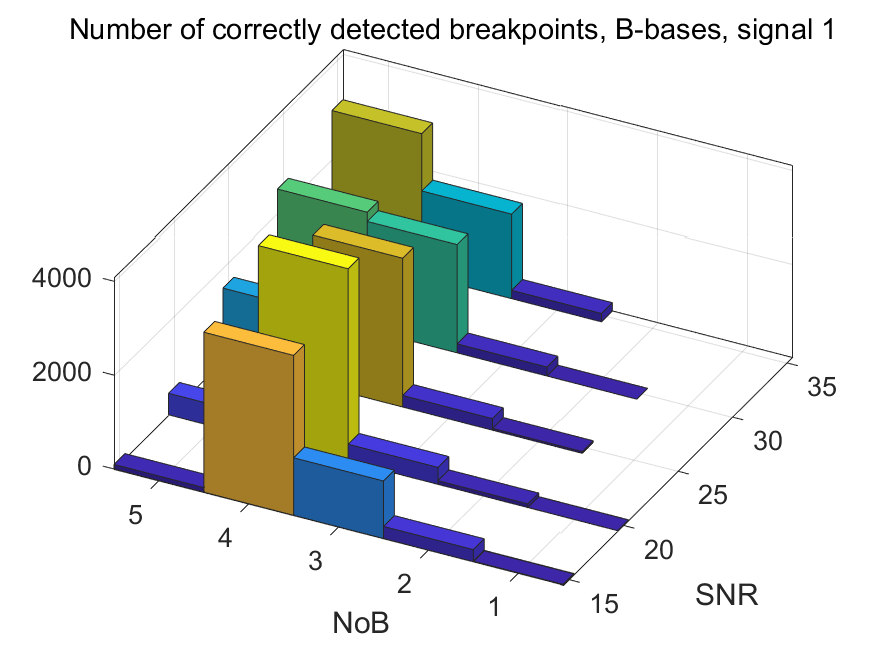
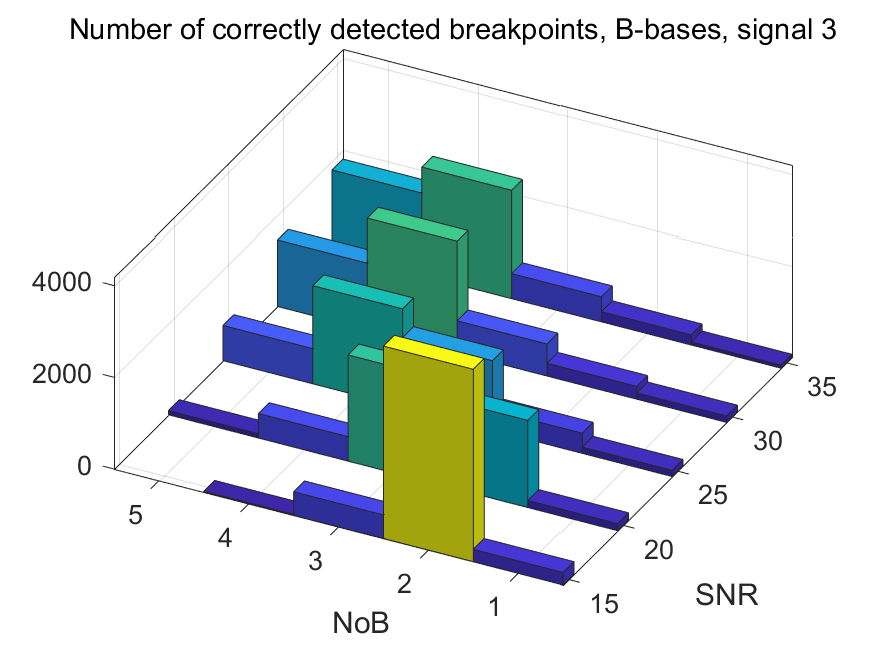
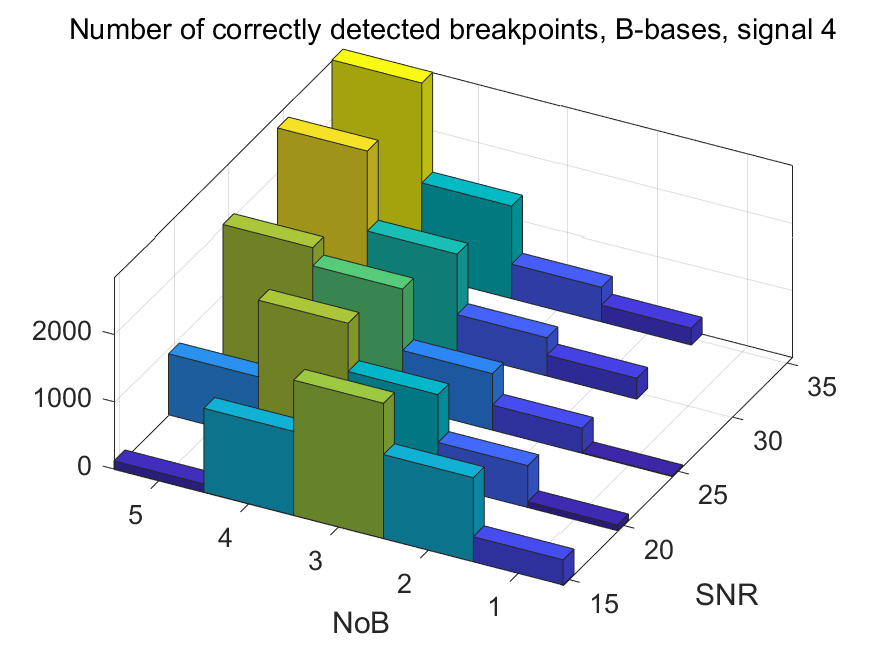
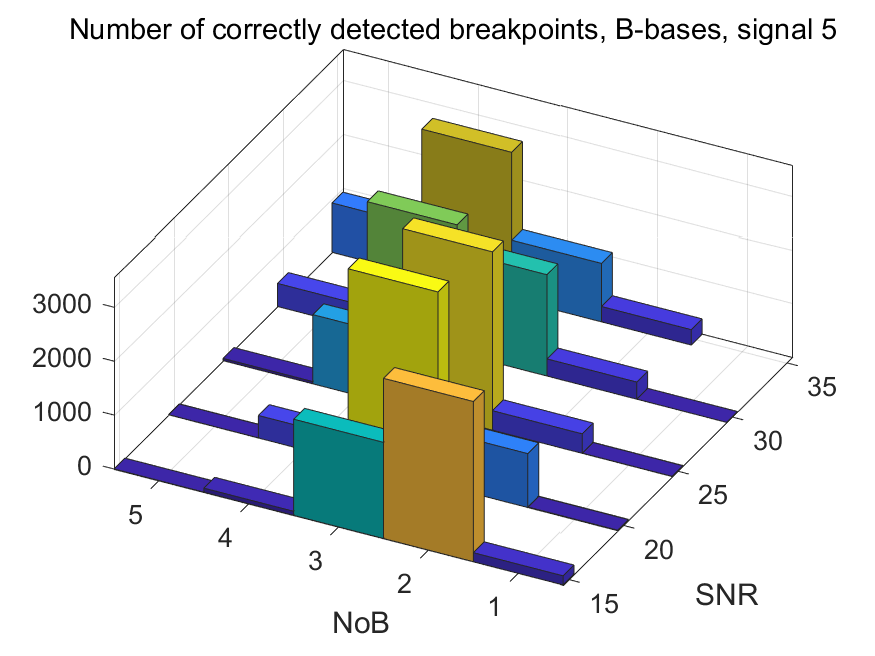
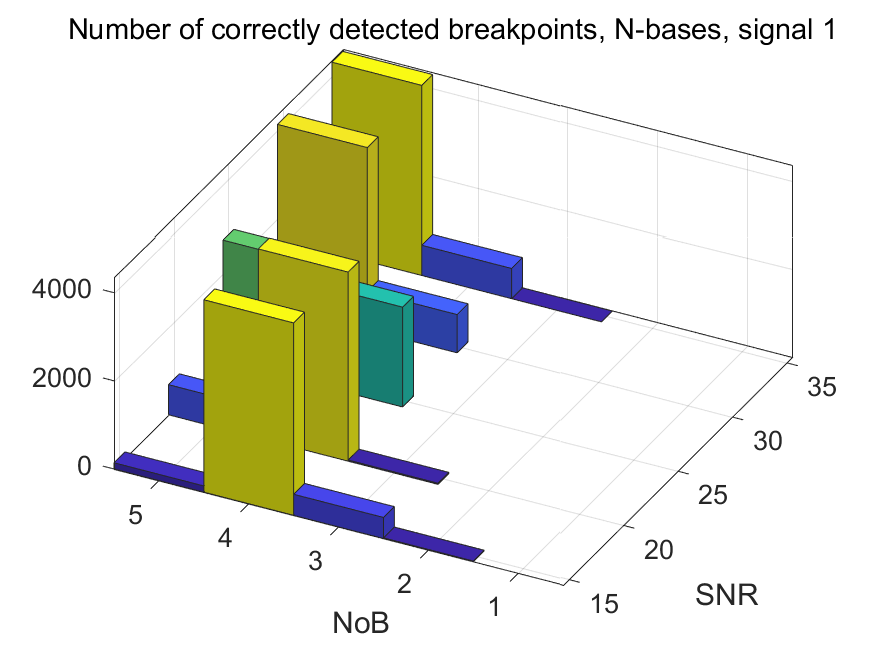
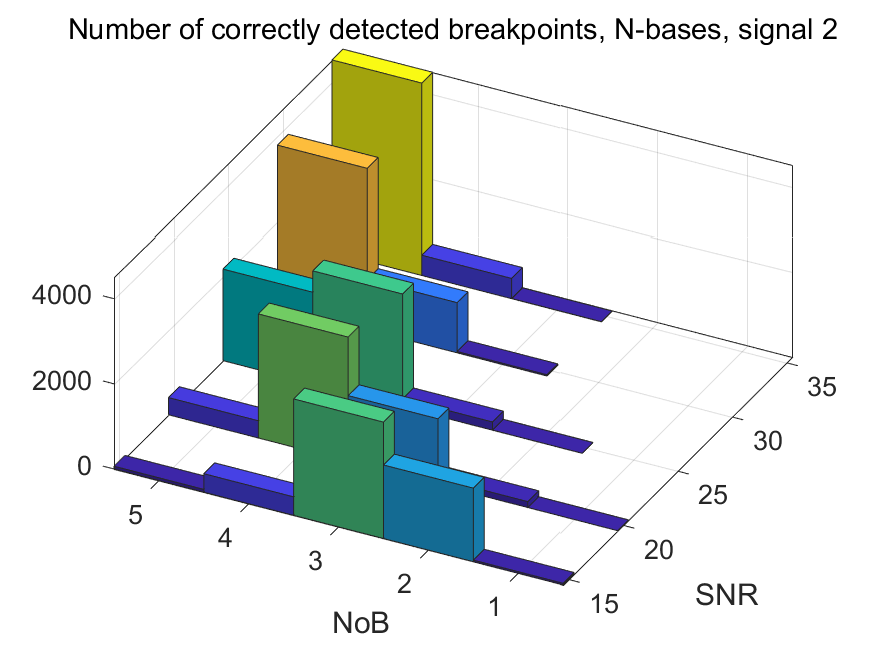
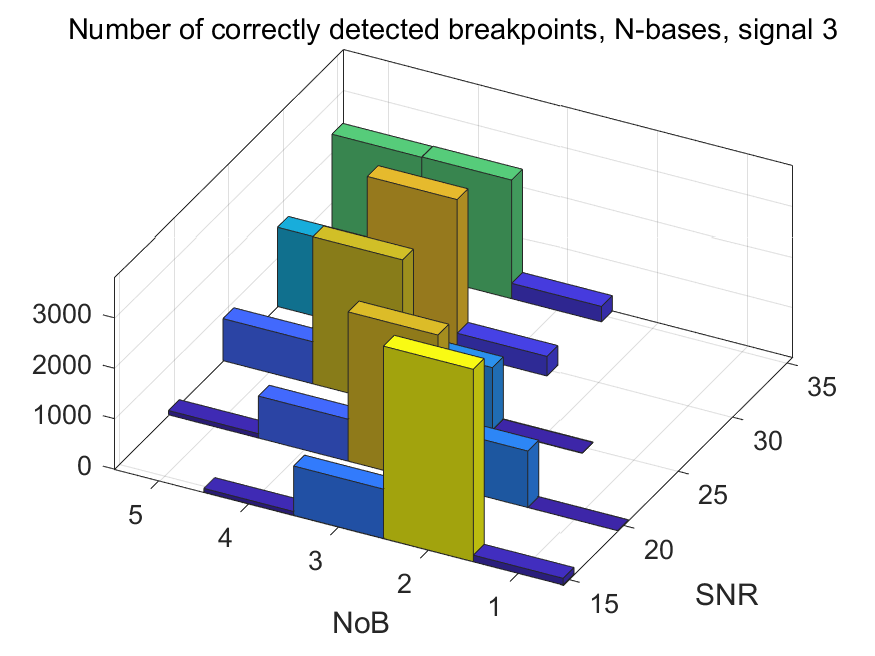
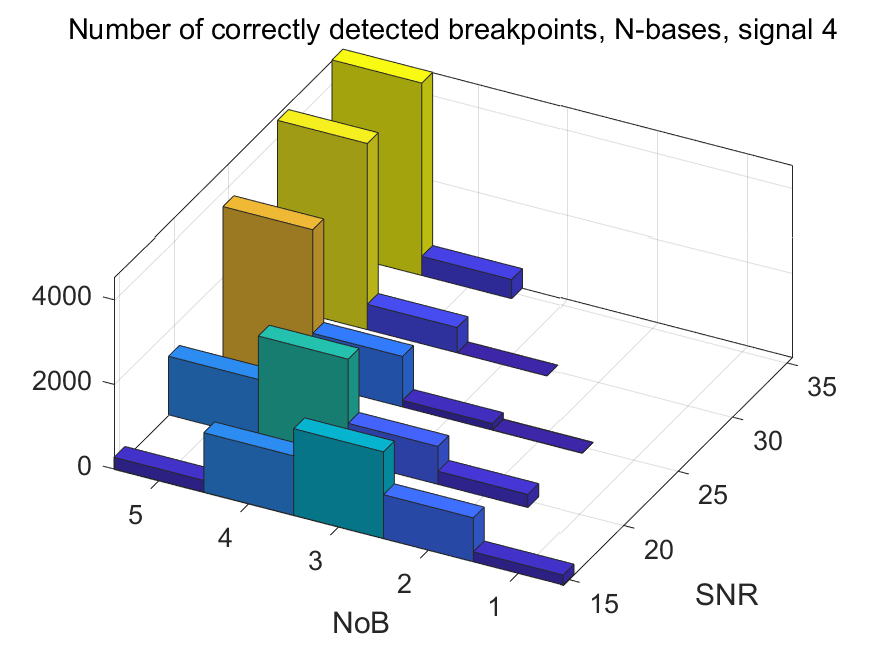
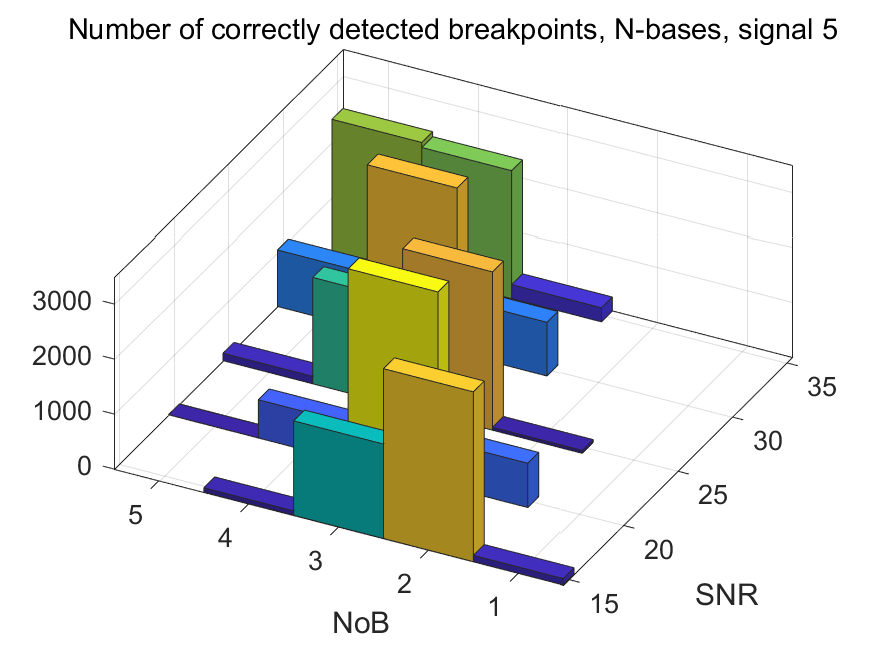
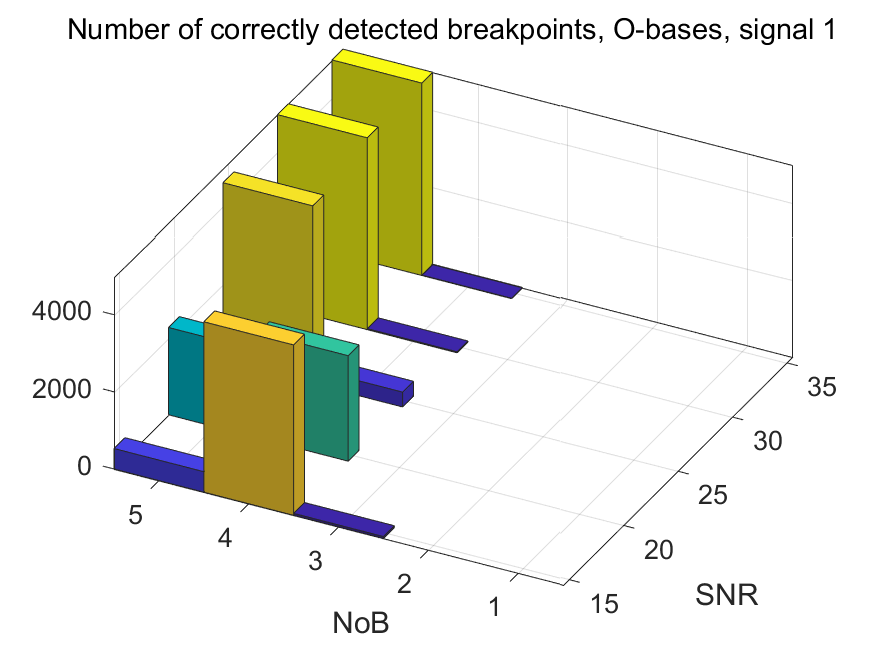
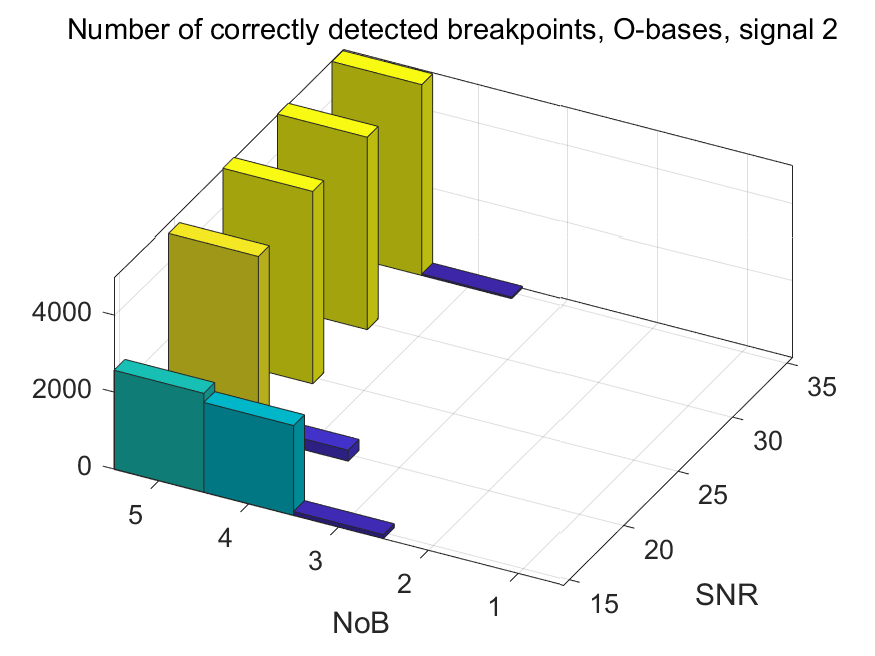
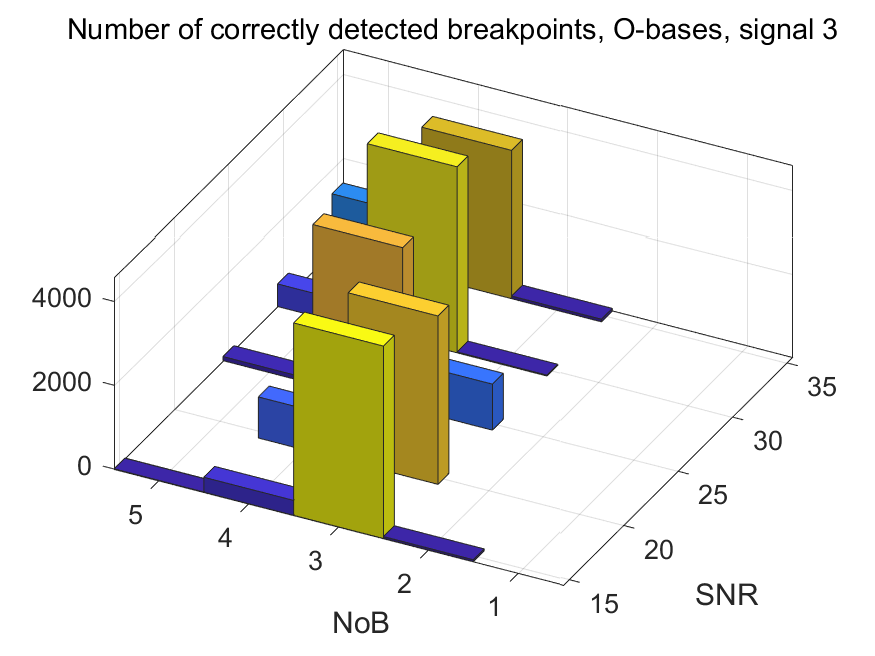
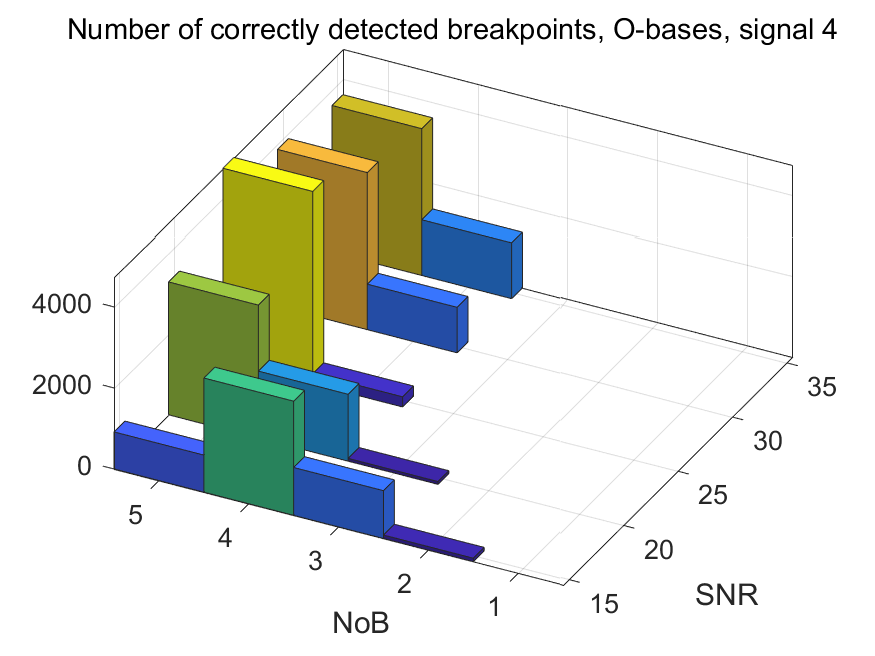
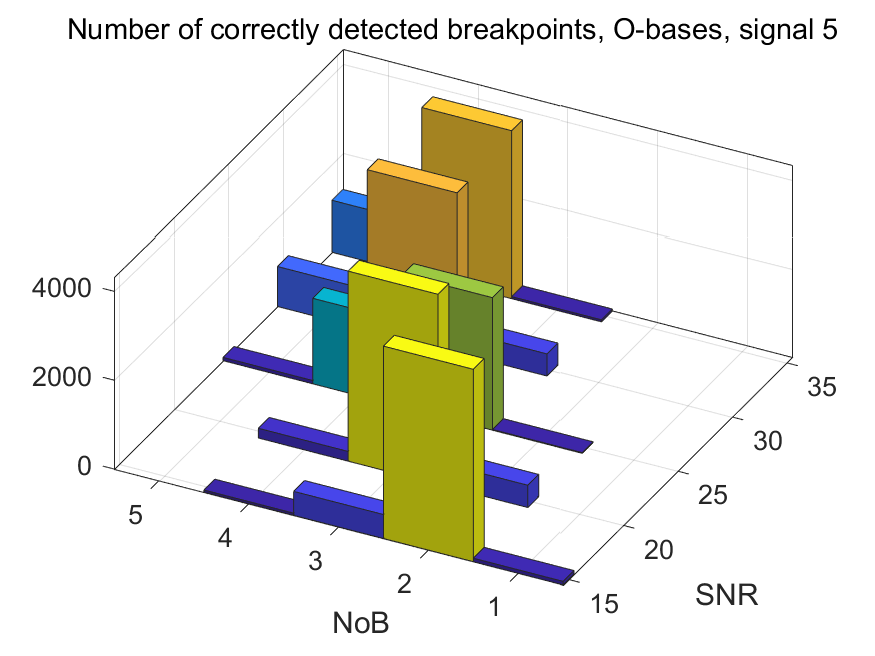
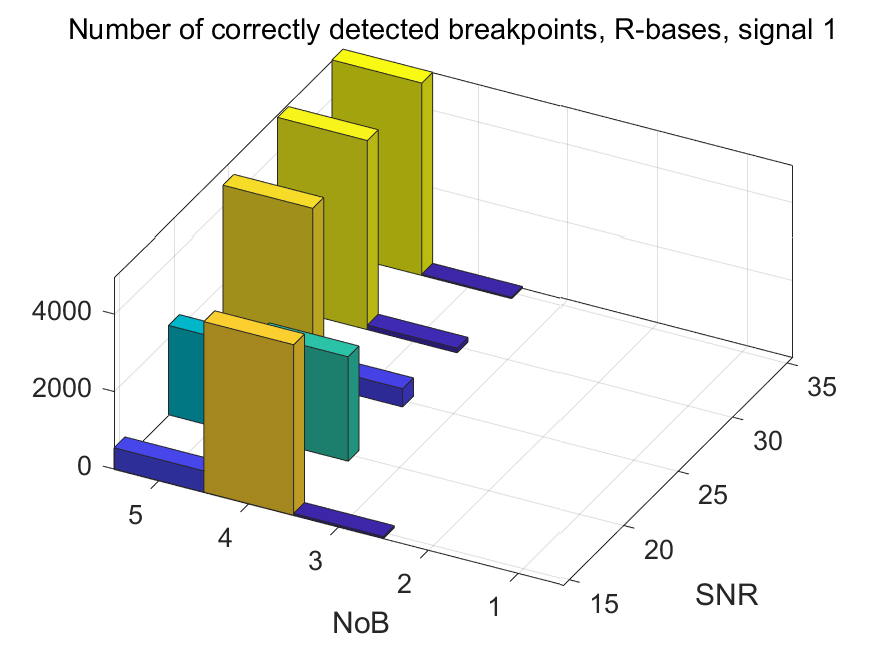
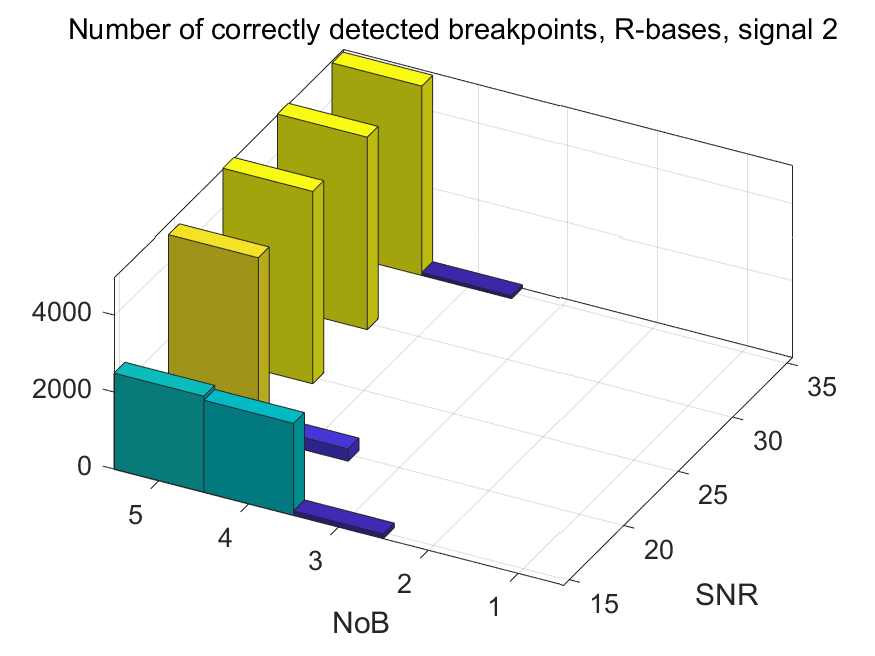
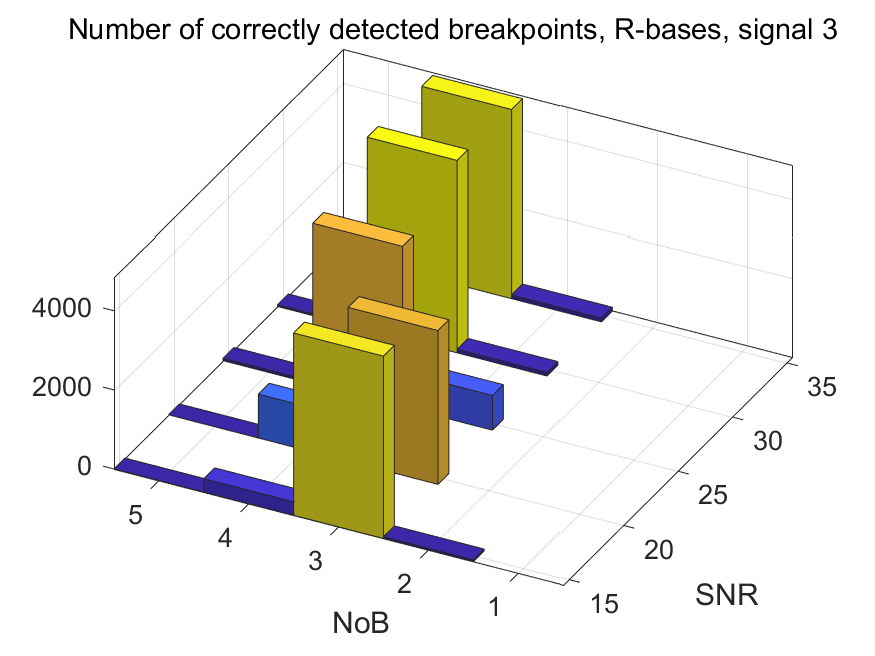
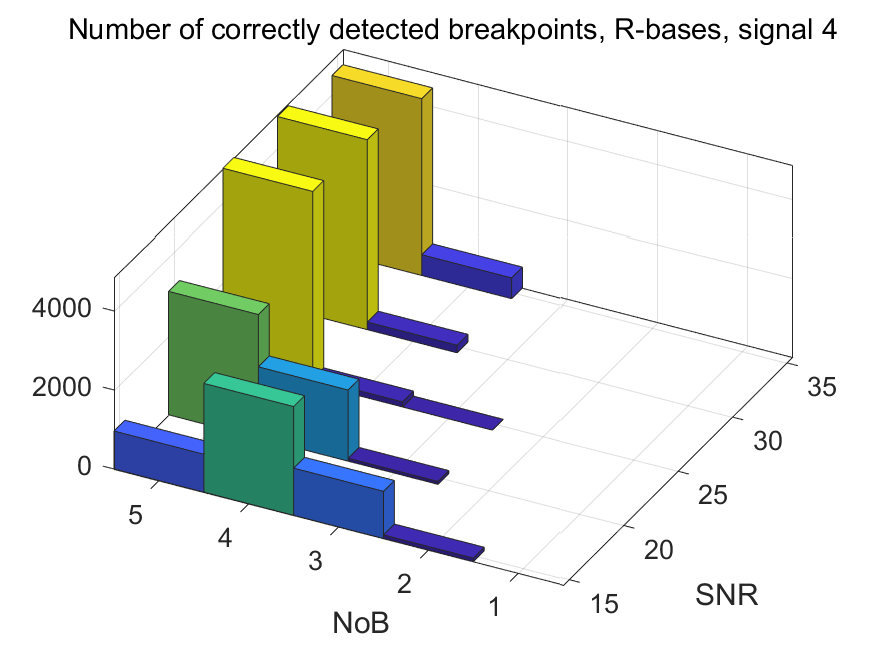
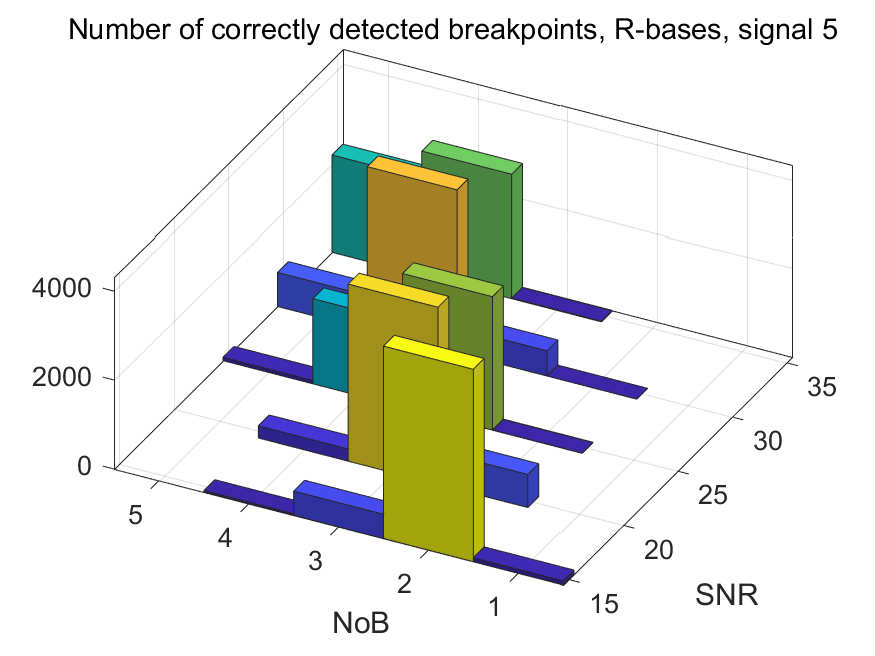
The NoB indicator in the form of 3D-histograms:

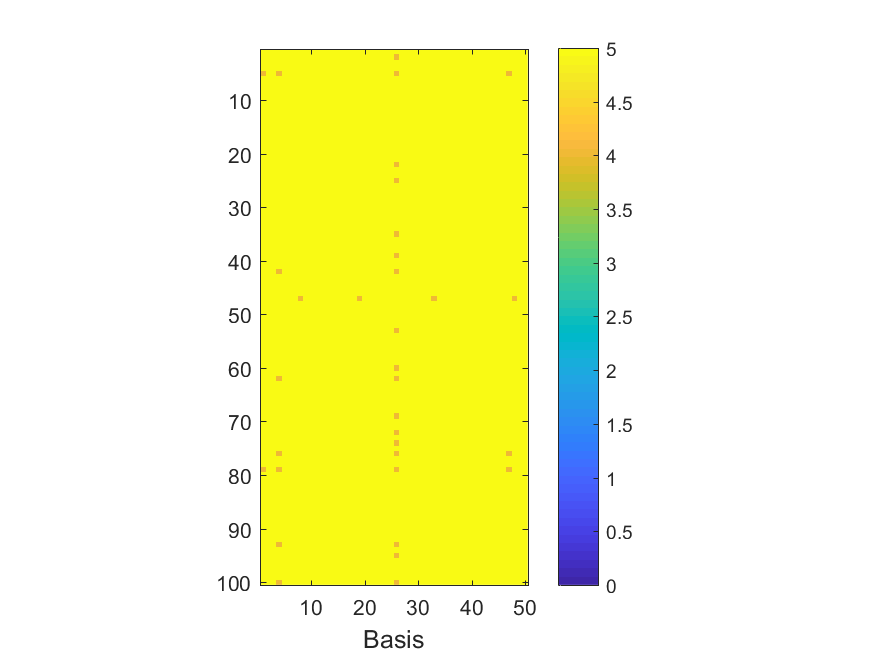
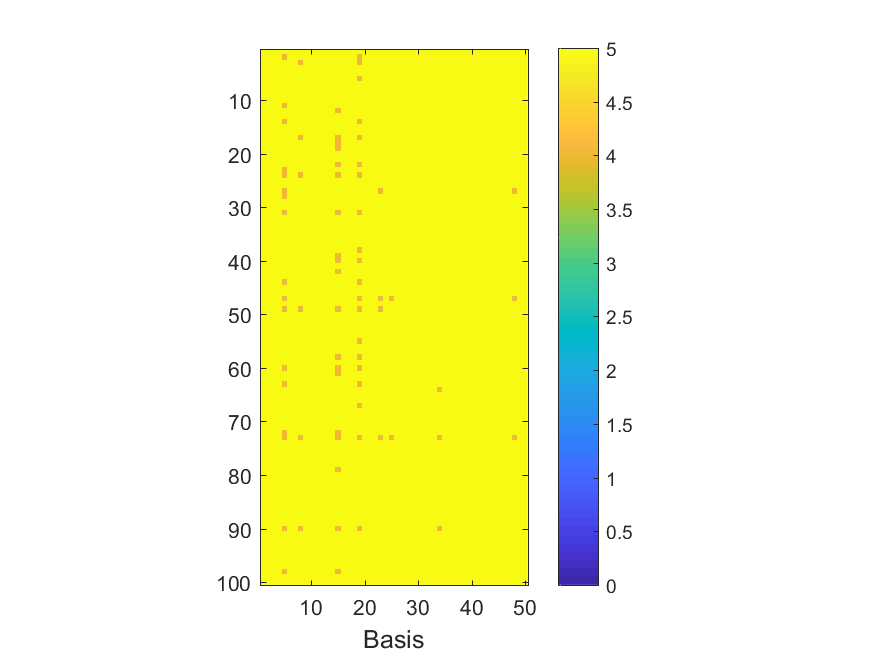
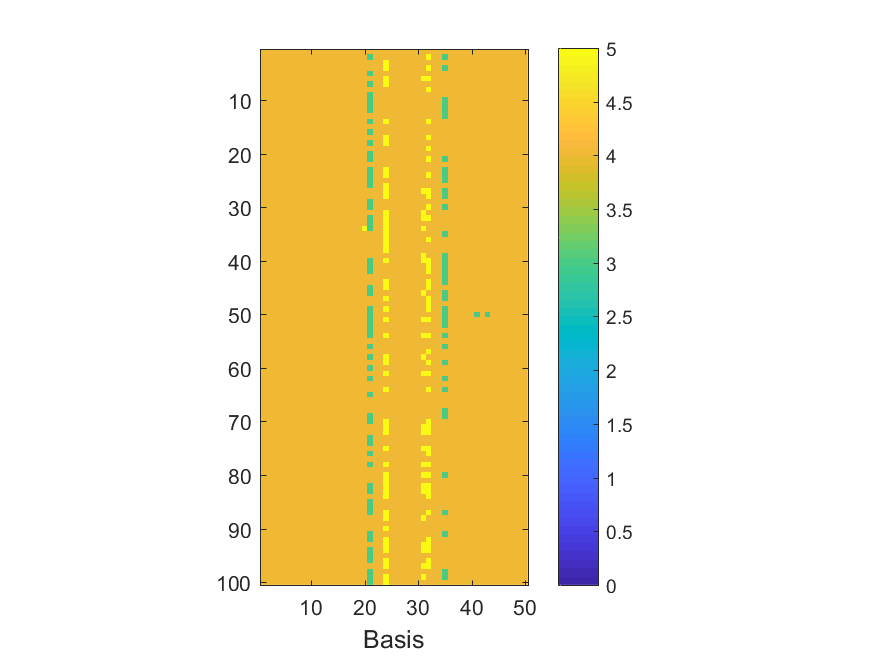
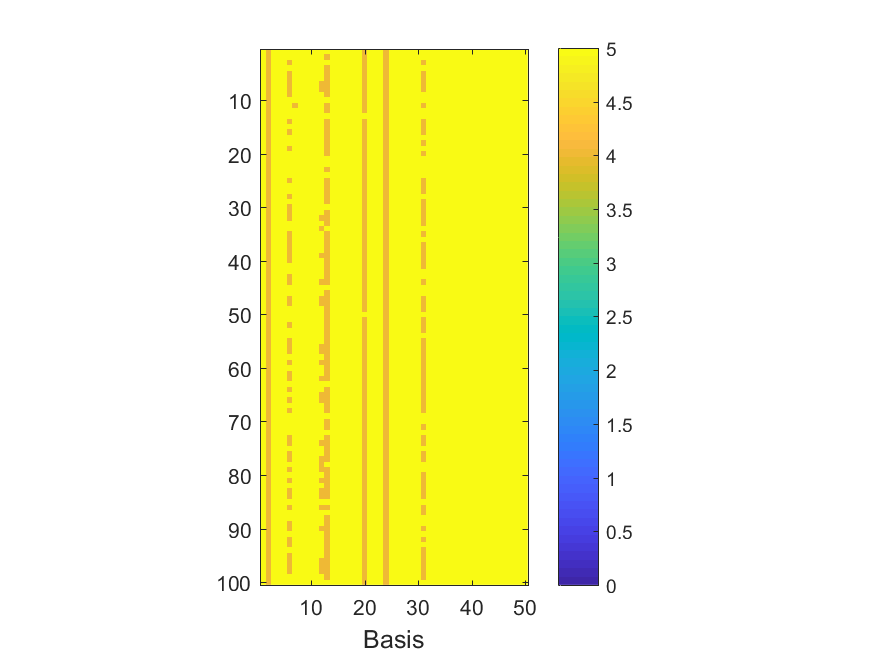
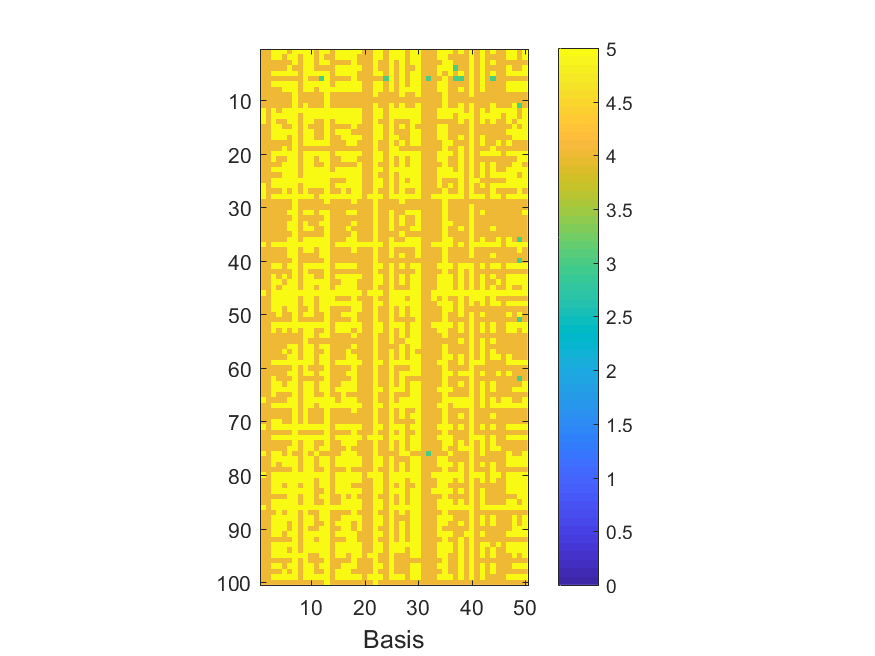
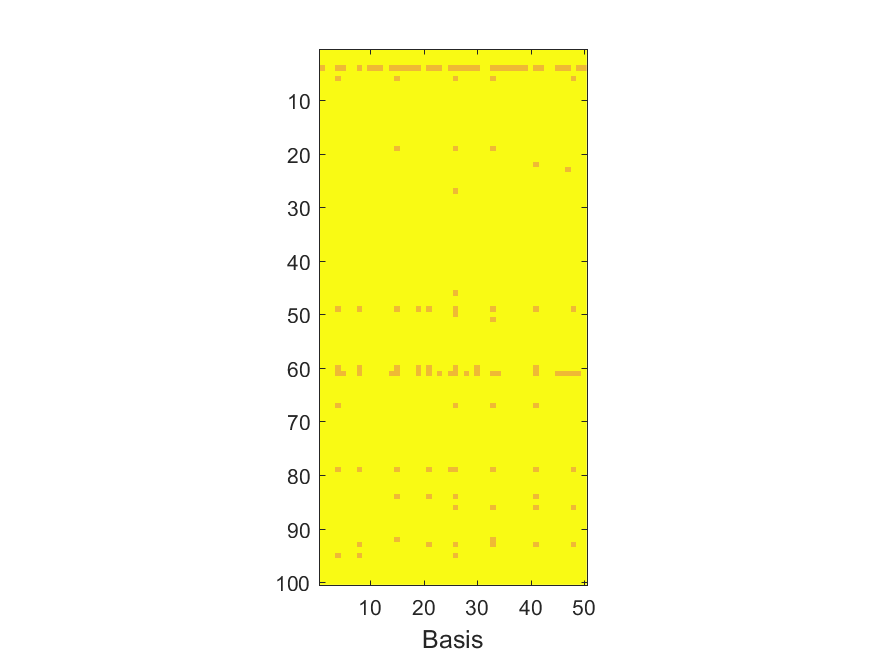
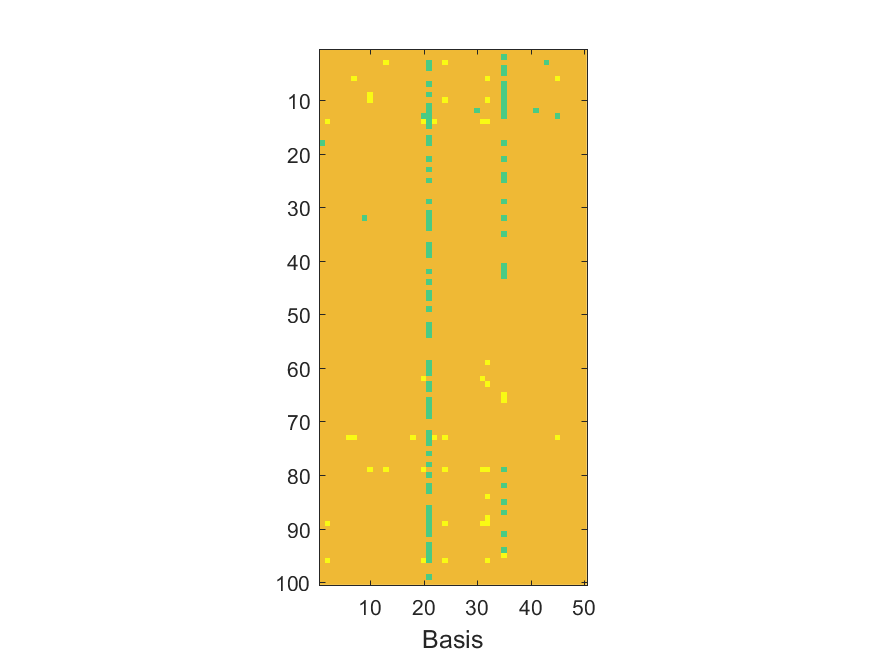
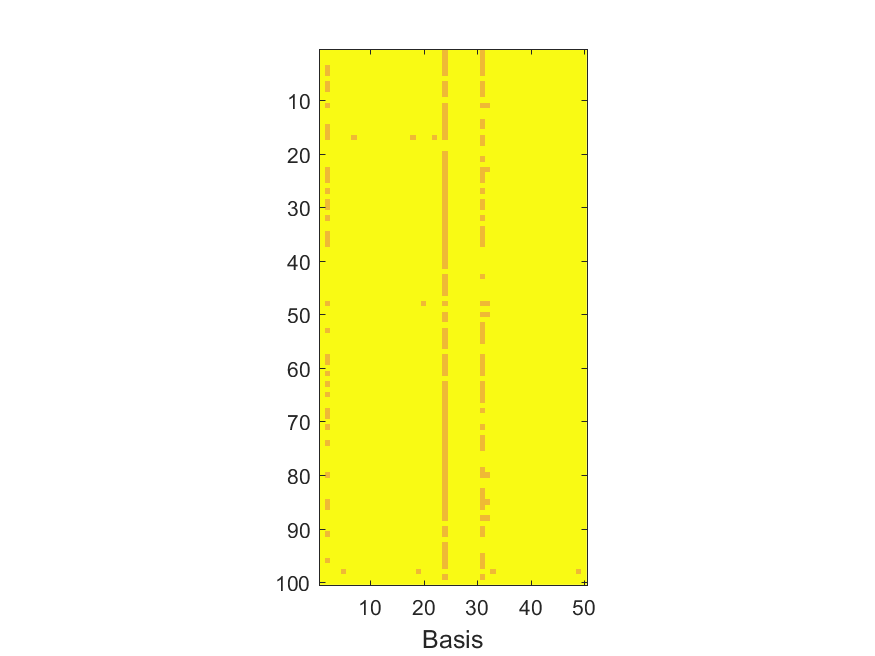
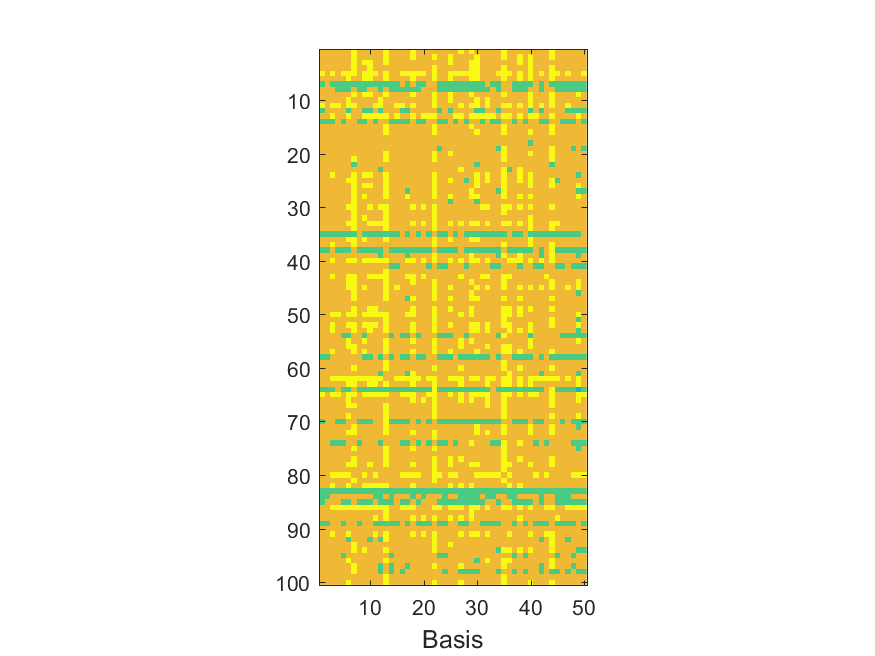
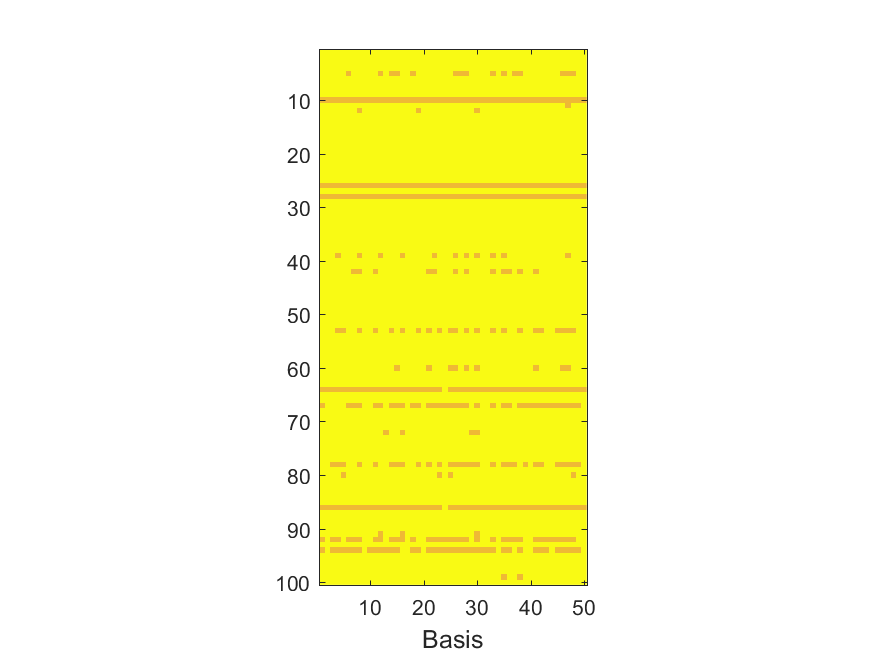
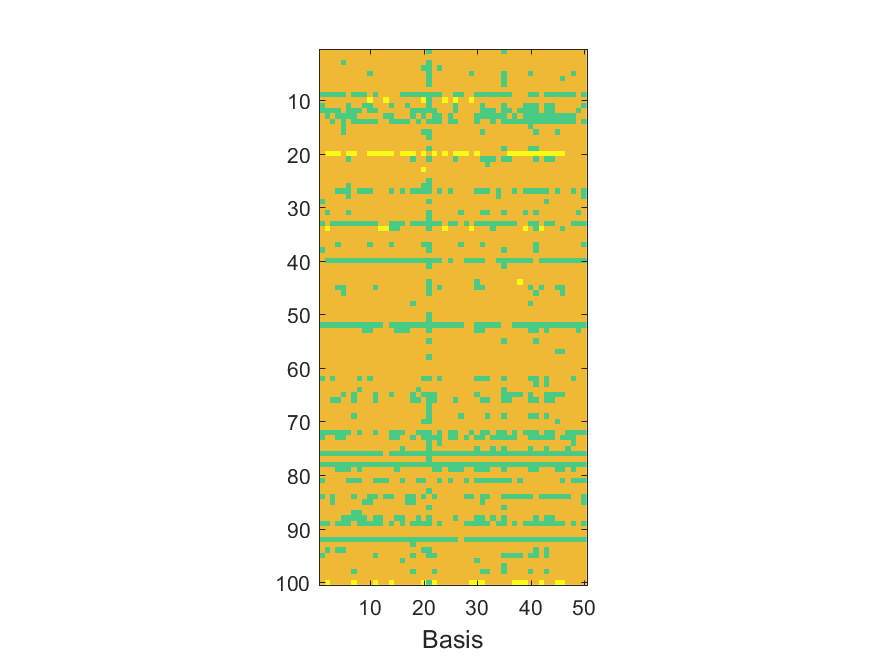
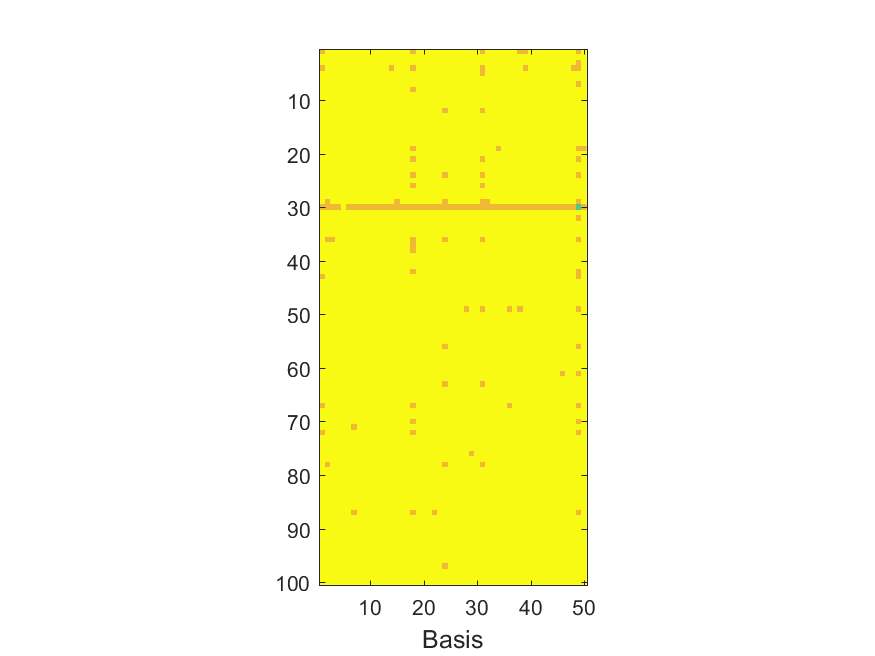
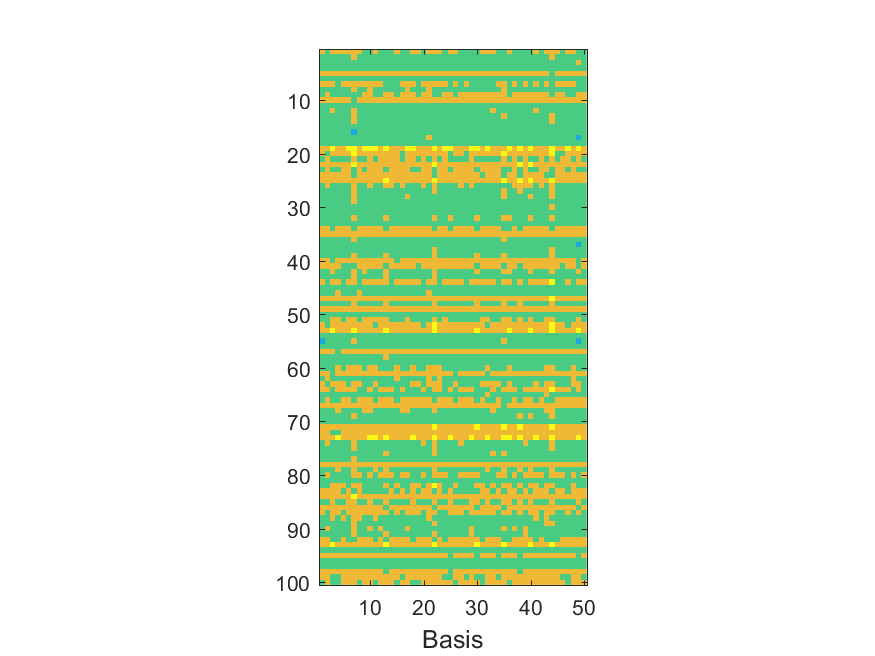
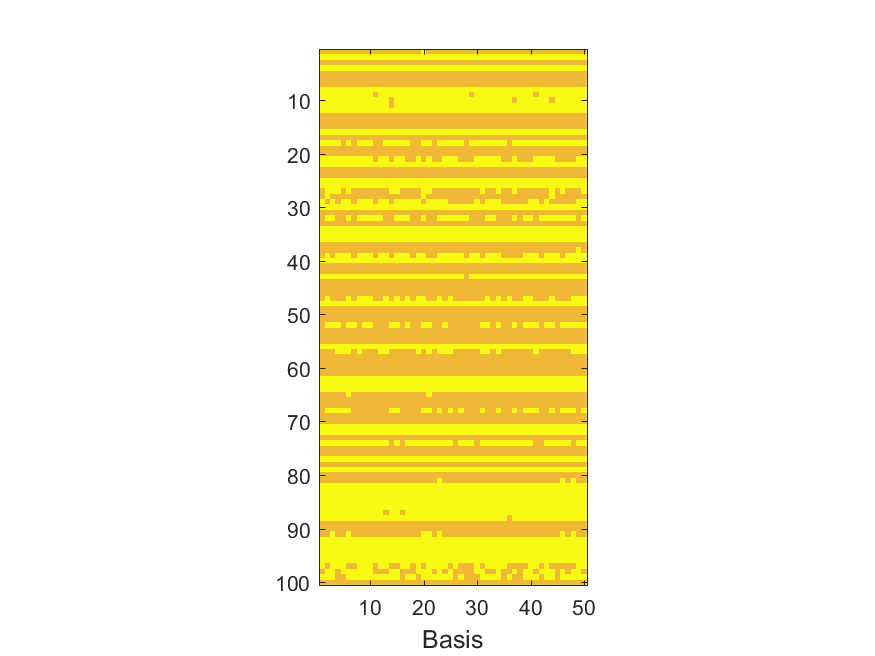
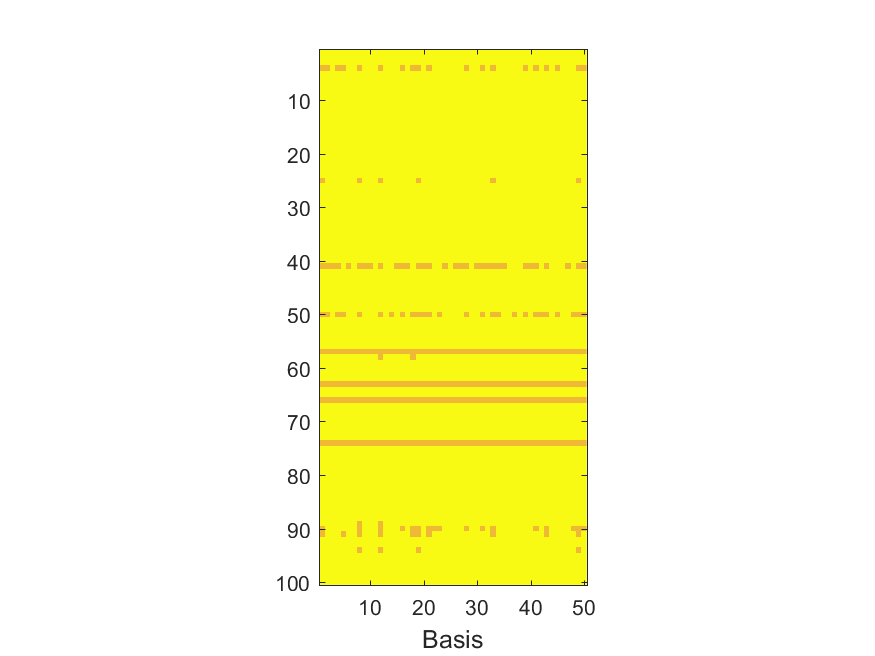
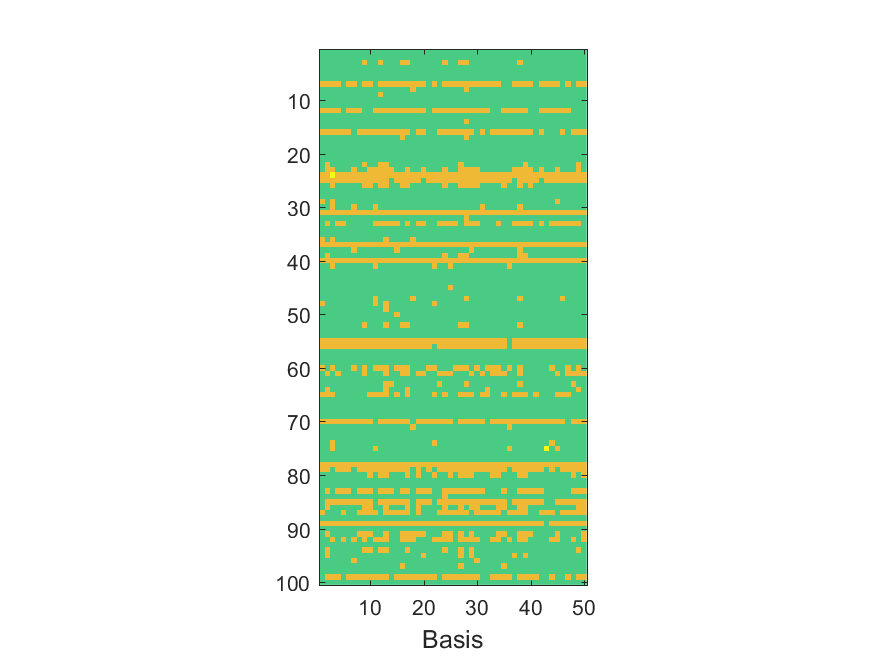
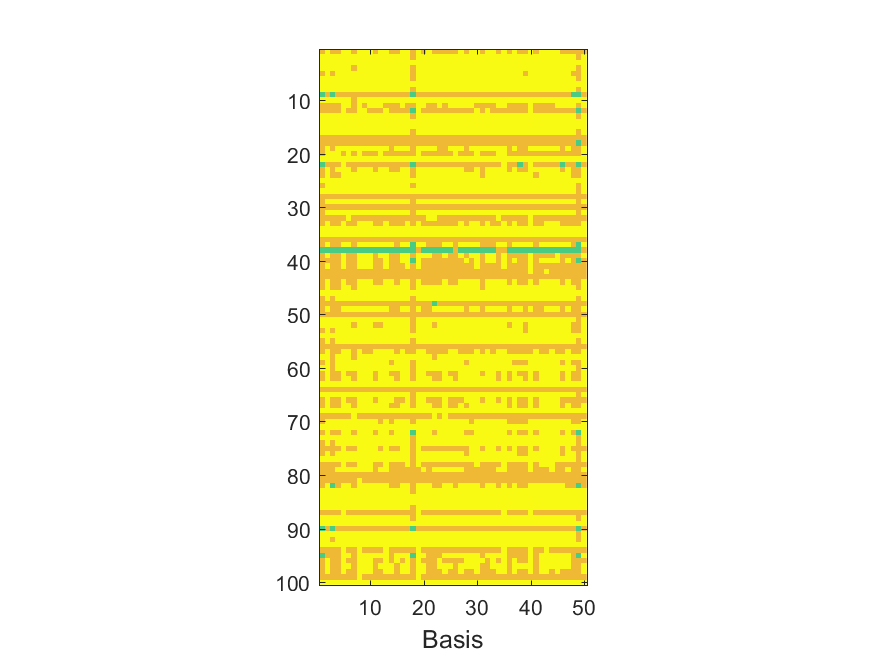
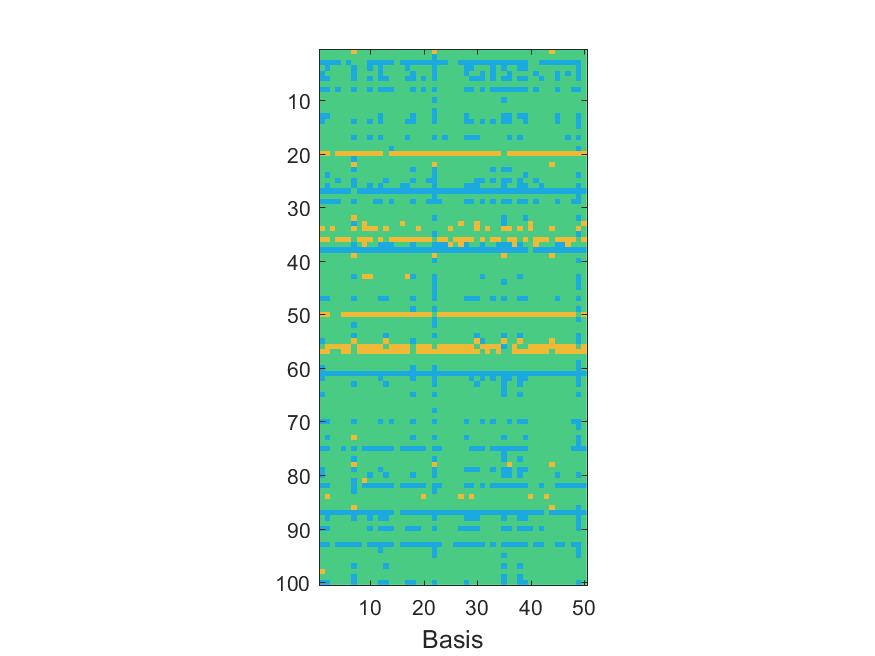
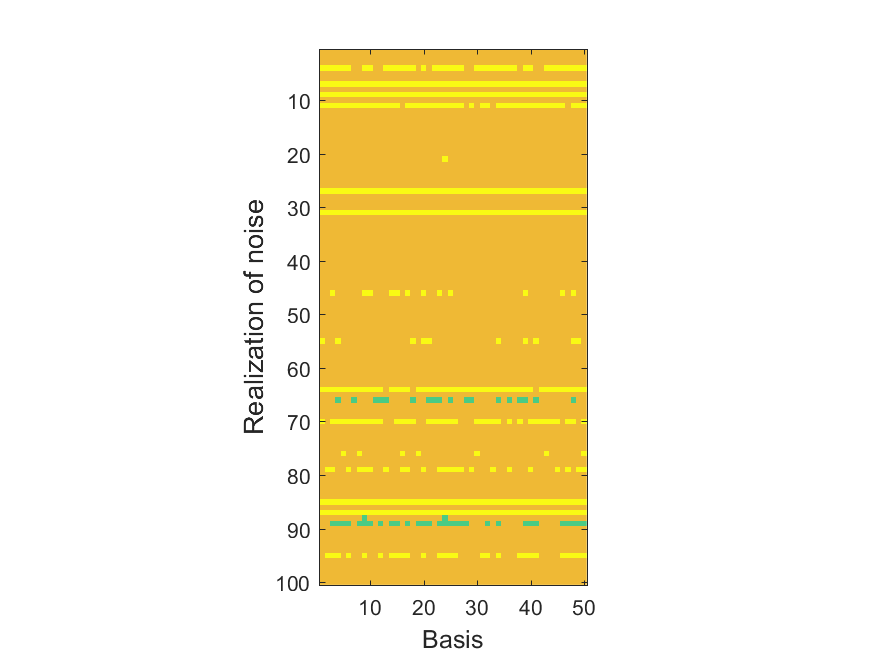
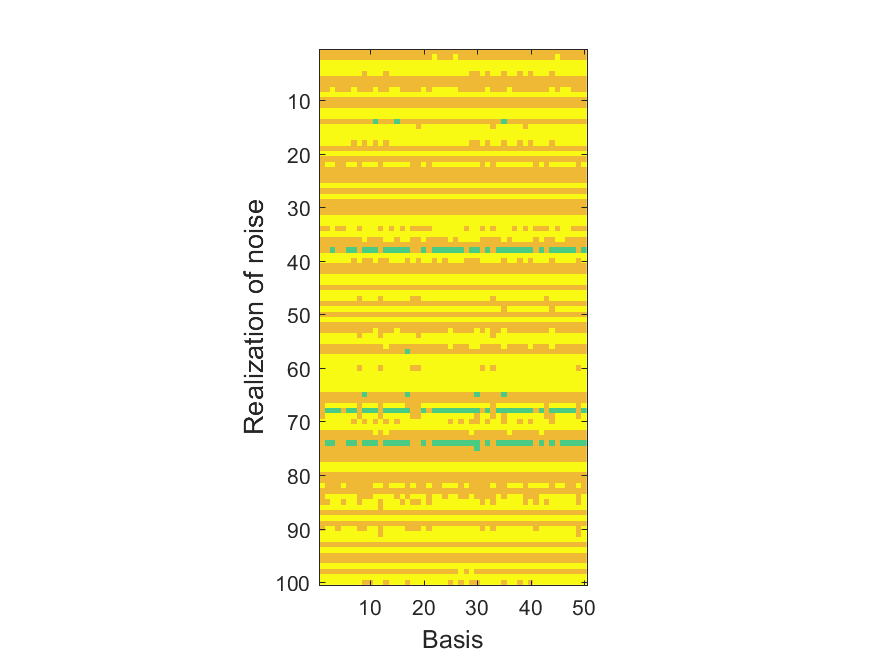
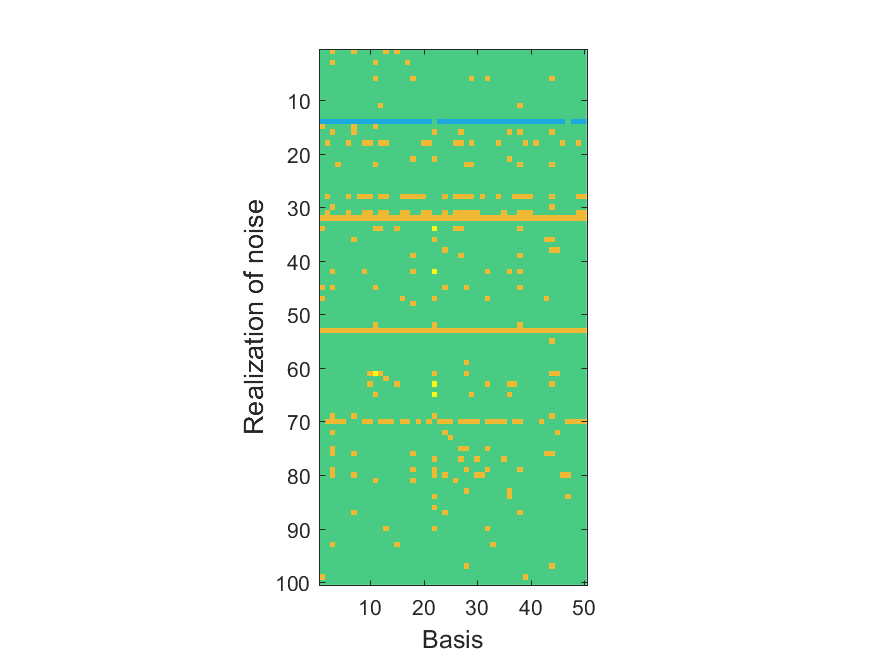
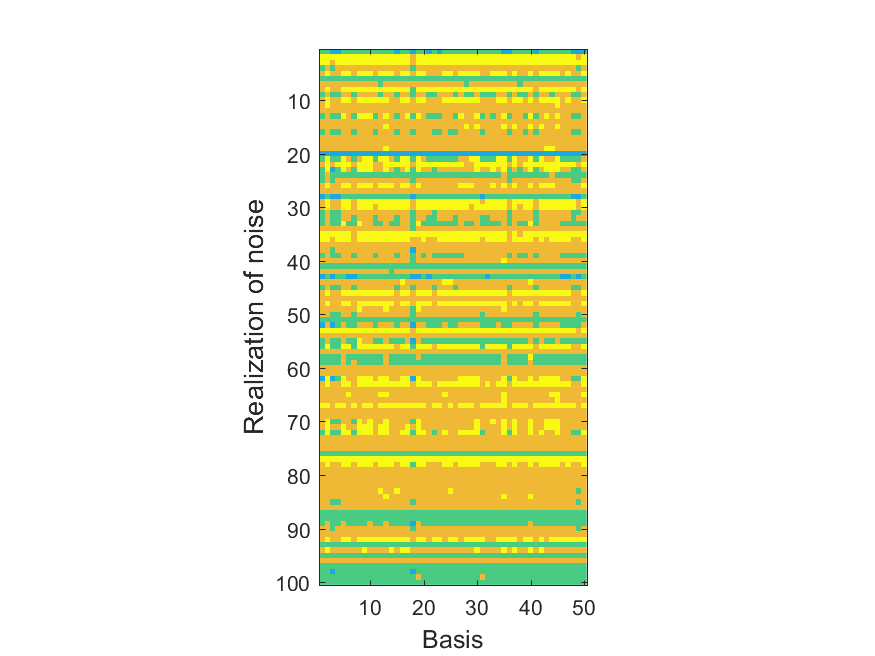
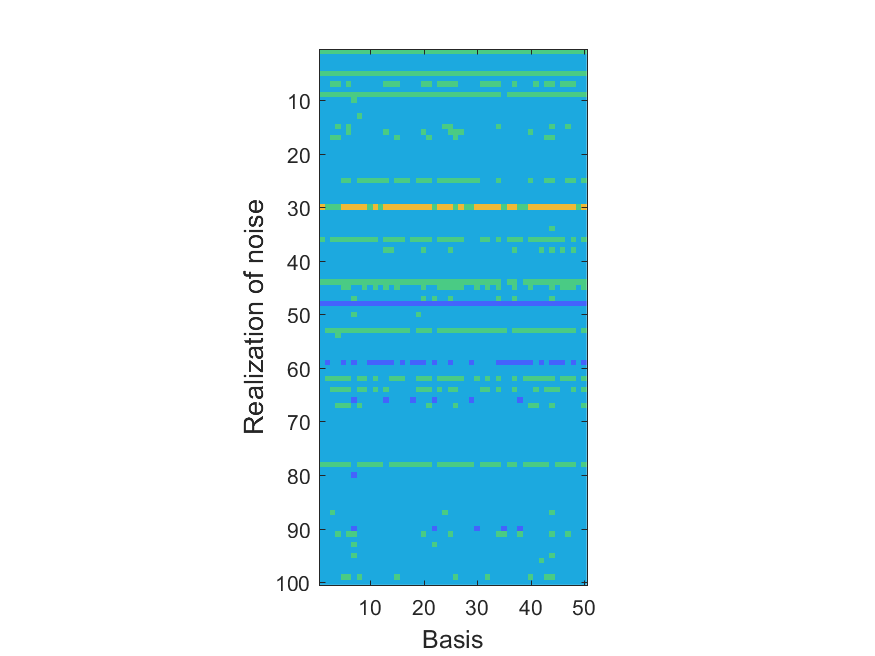
The NoB indicator for the particular combinations of bases and realizations of noise:

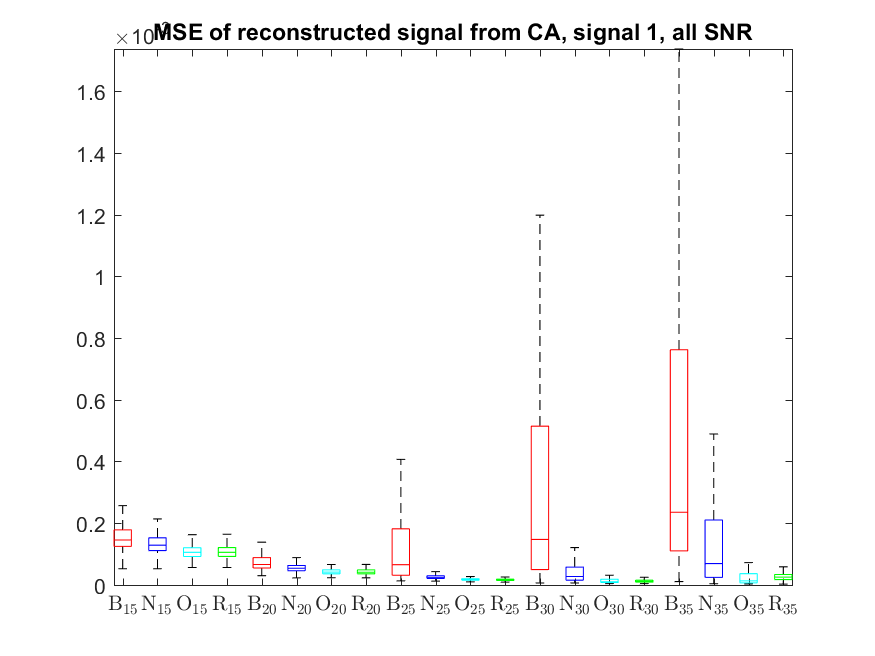
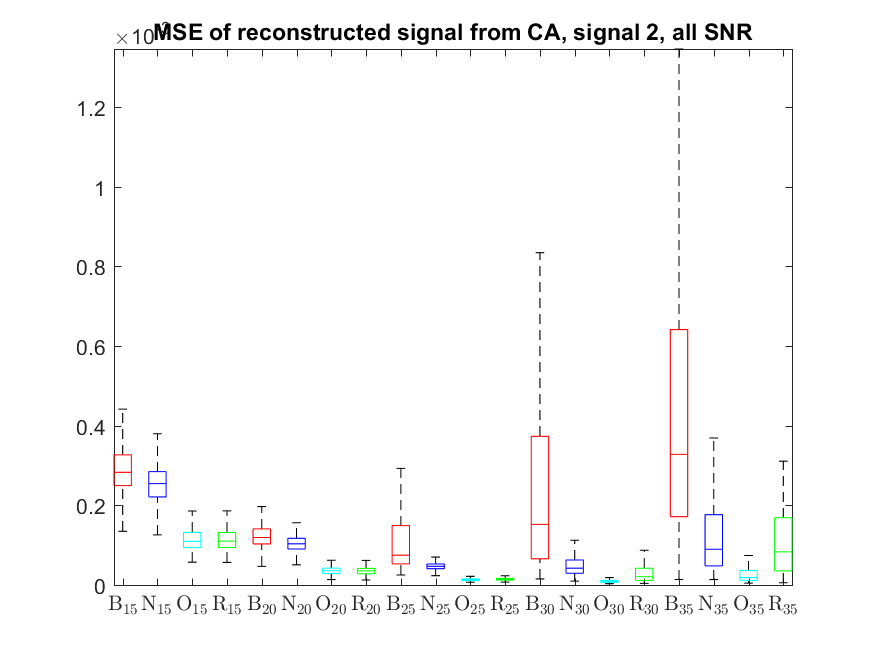
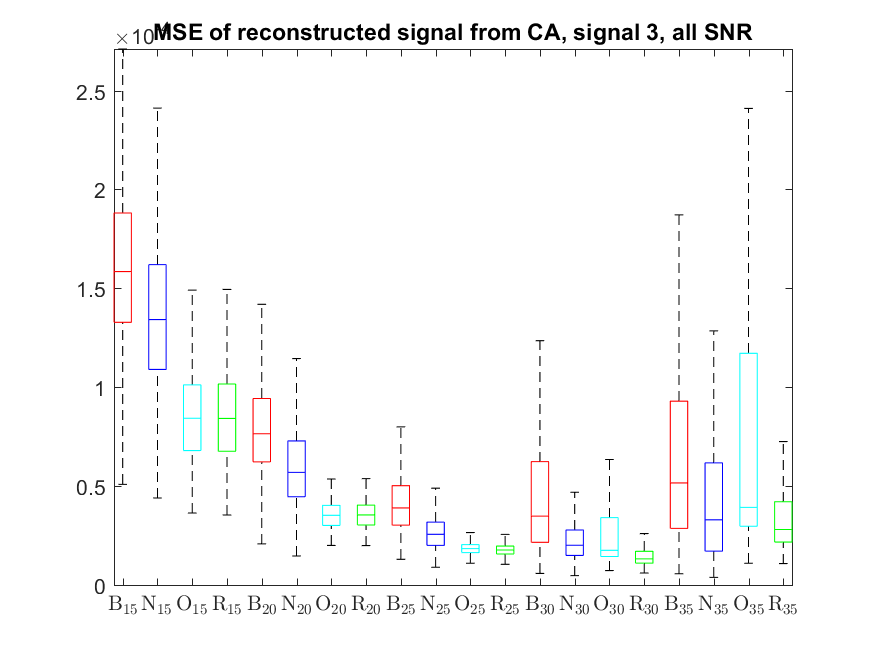
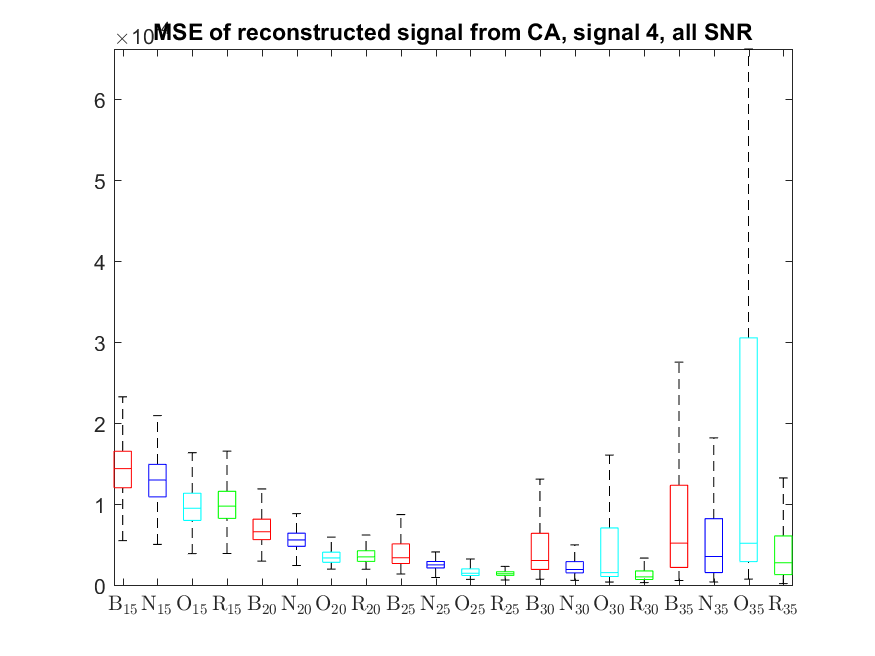
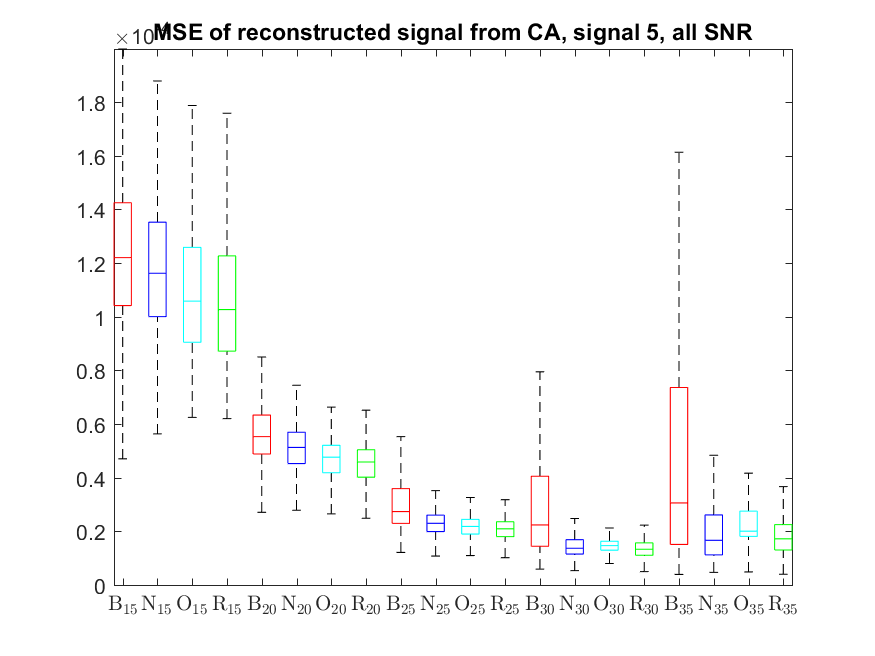
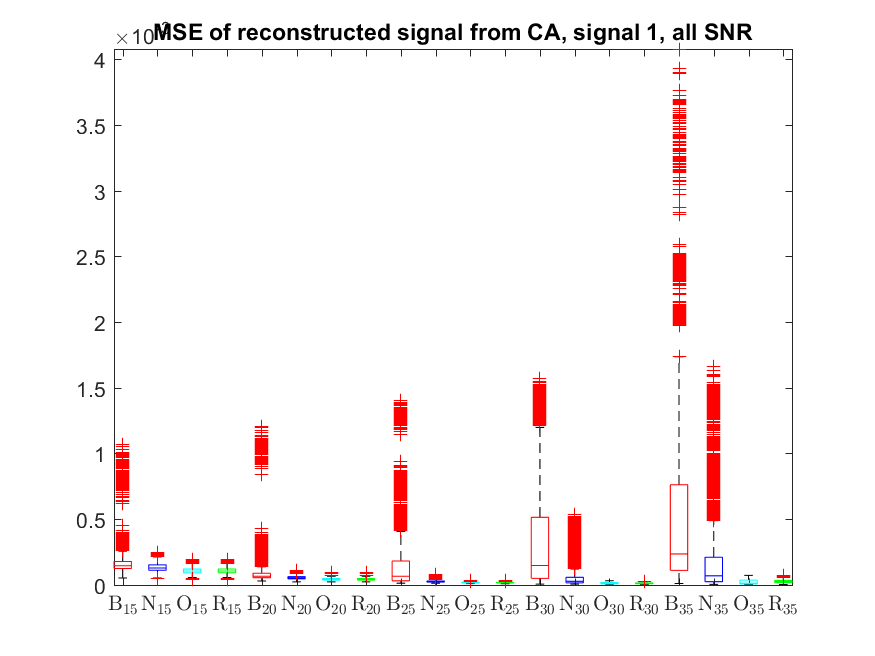
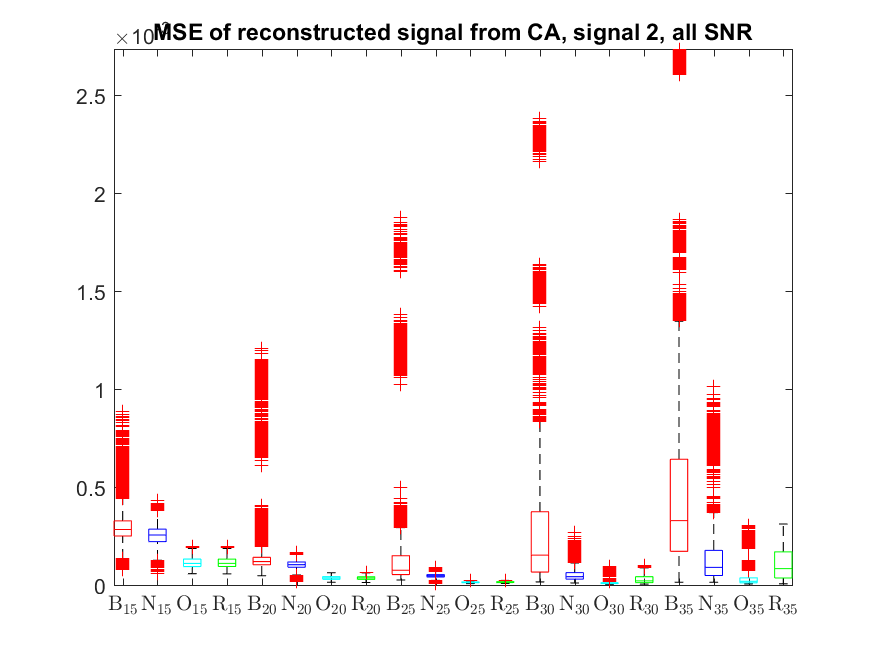
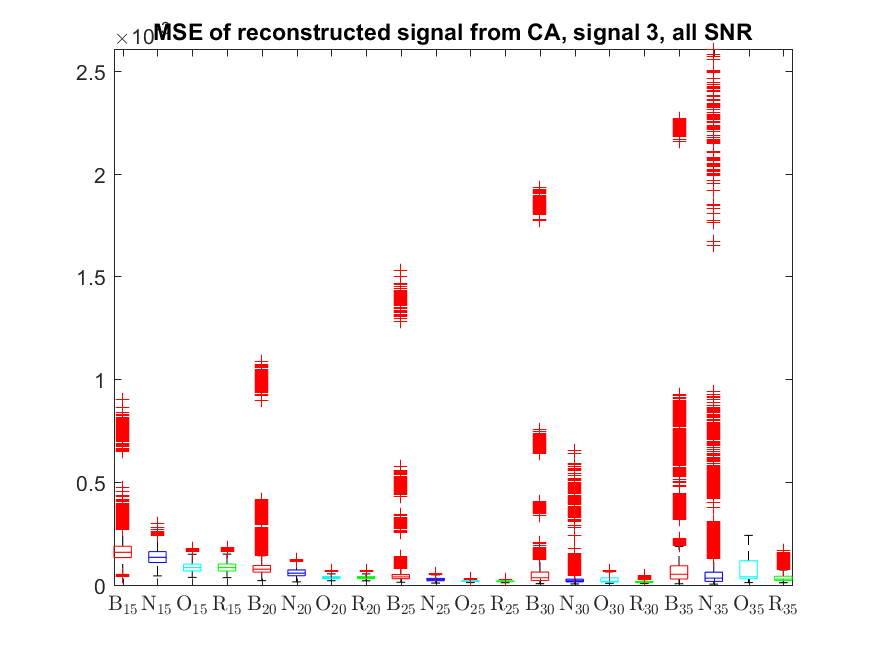
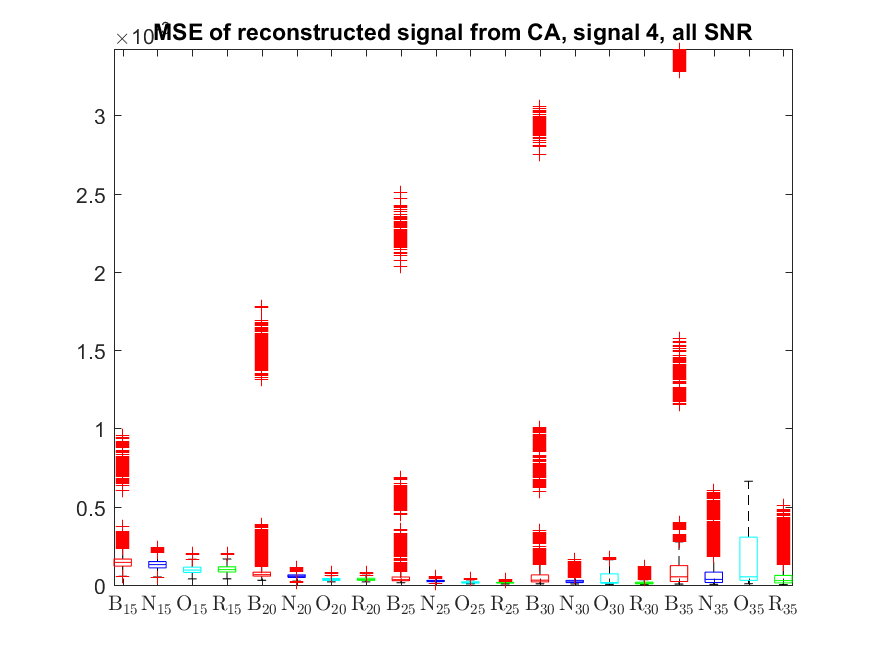
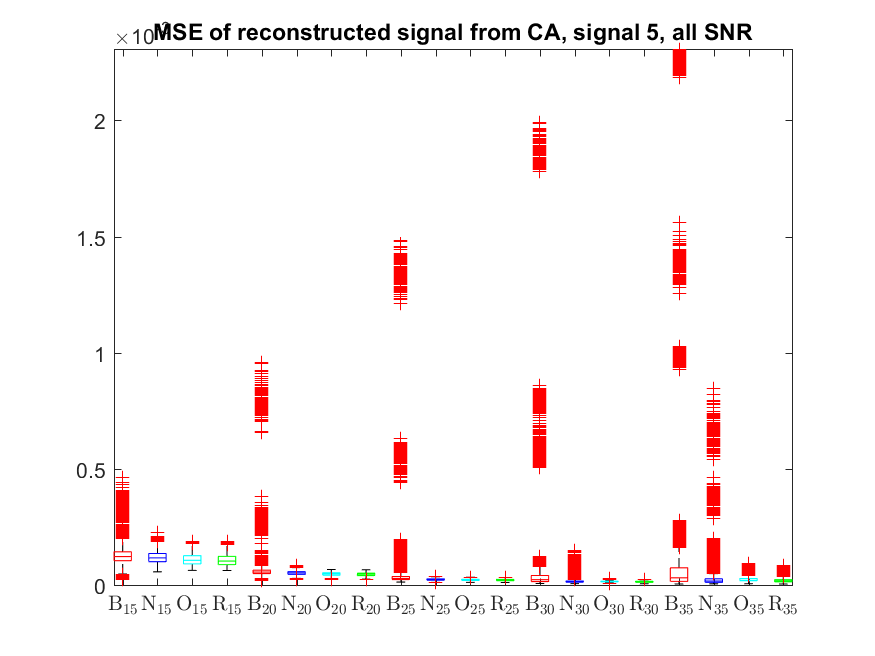
The MSE distributions when the signal is reconstructed directly from the output of the Condat algorithm (including and excluding outliers in the boxplots):

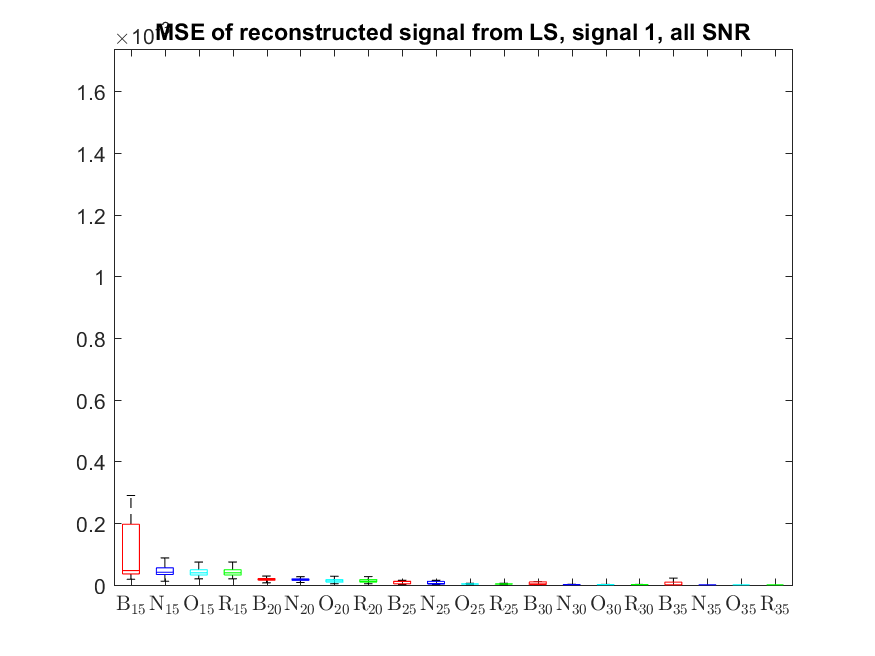
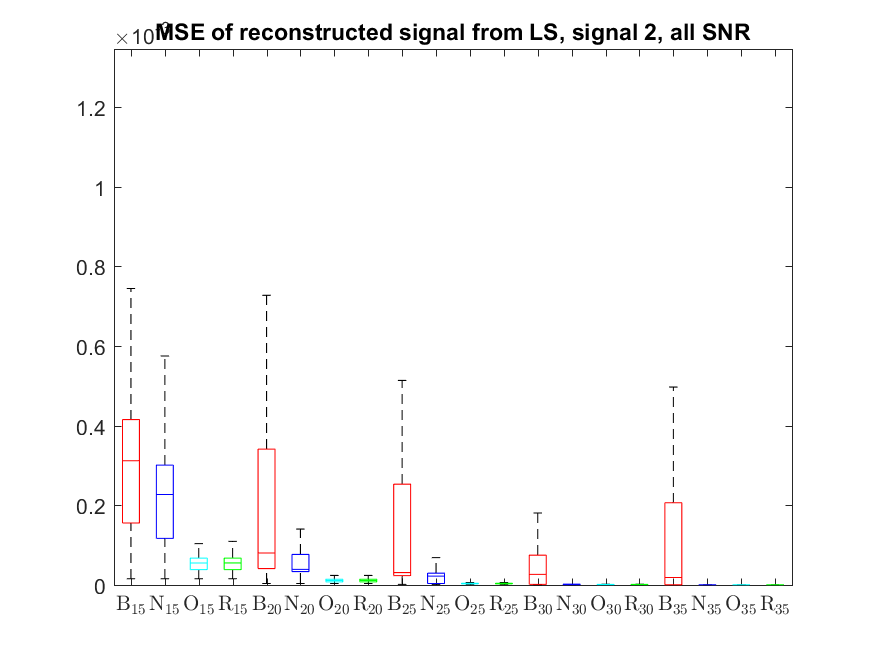
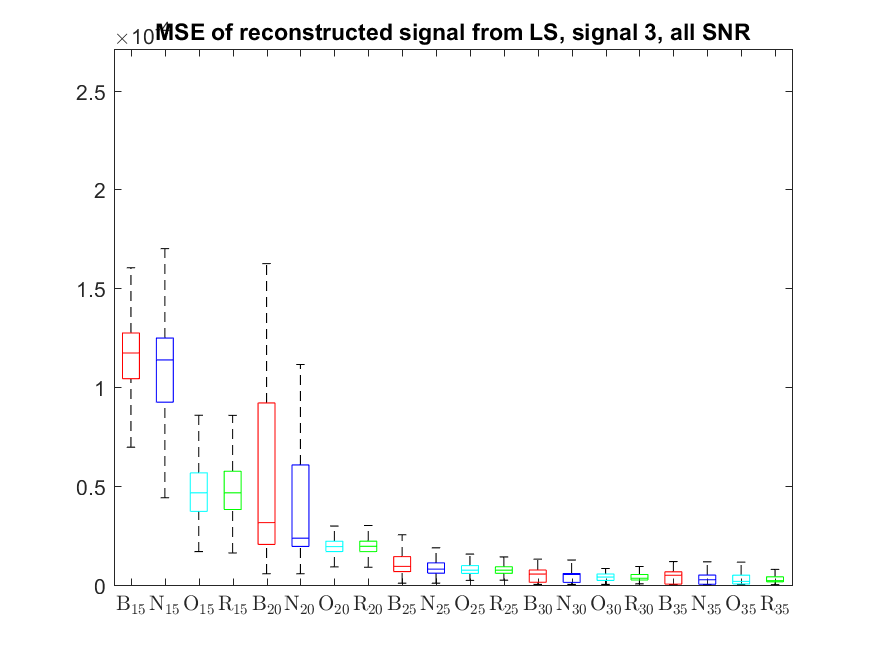
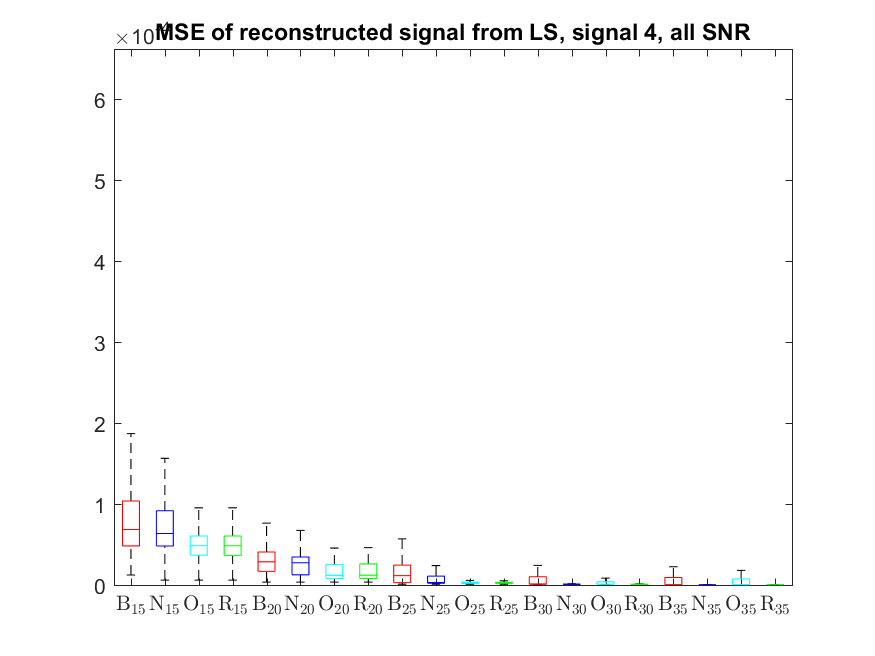
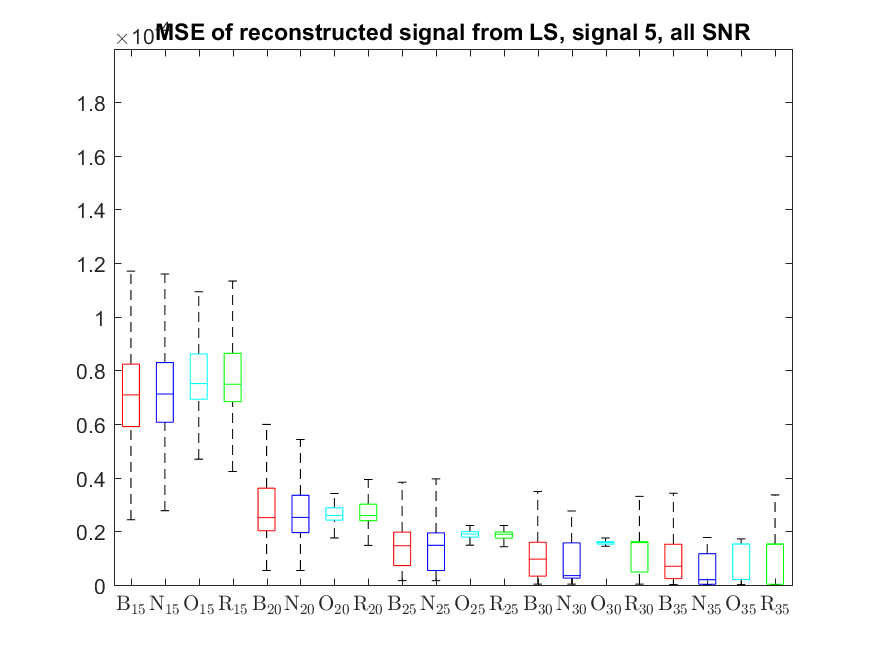
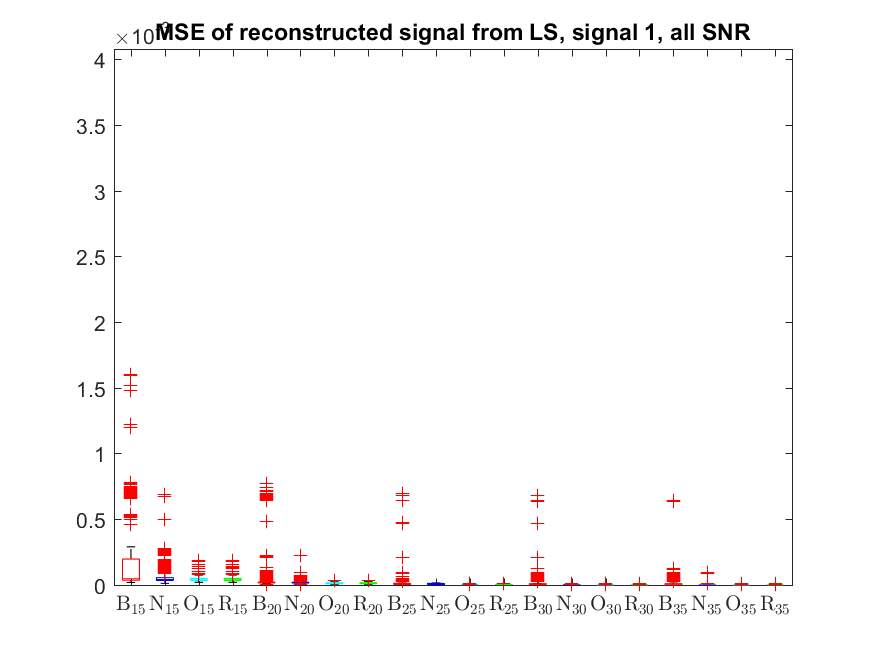
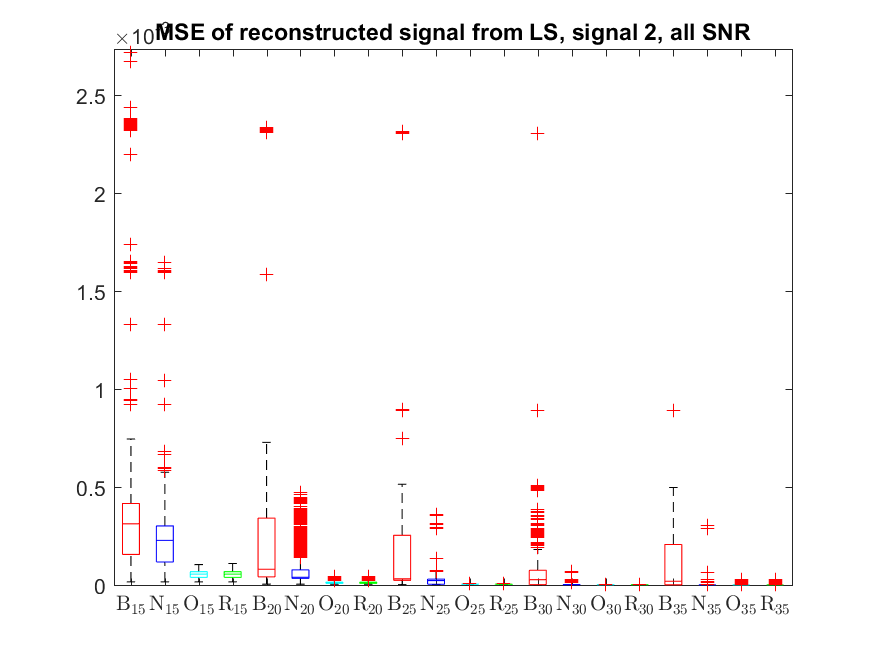
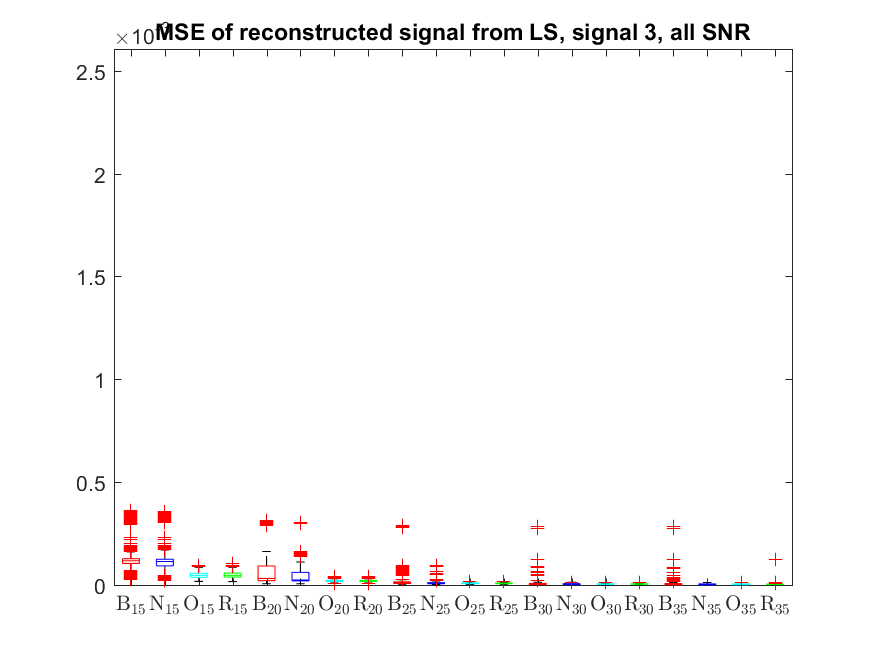
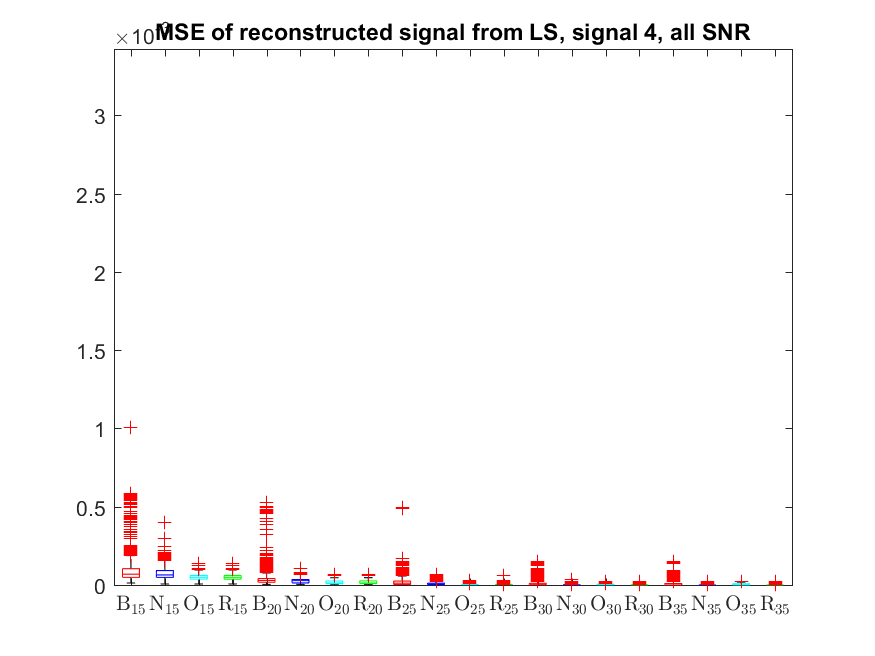
The MSE distributions when the signal is reconstructed by the additional least squares, i.e. debiased (including and excluding outliers in the boxplots). The plots that match the corresponding CA cases have identical scale for easier comparison: